题目内容
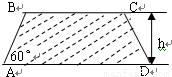
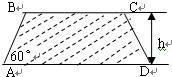 建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为6
建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为6| 3 |
(1)求外周长的最小值,此时防洪堤高h为多少米?
(2)如防洪堤的高限制在[ 3 , 2
| 3 |
分析:(1)利用梯形的面积公式将梯形的上底、下底用h表示;将梯形周长用h表示;利用基本不等式求出周长的最小值.
(2)利用函数单调性的定义判断出函数的单调性;利用函数的单调性求出周长的最小值.
(2)利用函数单调性的定义判断出函数的单调性;利用函数的单调性求出周长的最小值.
解答:解:(1)6
=
(AD+BC)h,AD=BC+2×hcot60°=BC+
h,6
=
(2BC+
h)h,解得BC=
-
h.
设外周长为l,则l=2AB+BC=
+
-
h=
h+
≥6
;
当
h=
,即h=
时等号成立.外周长的最小值为6
米,此时堤高h为
米.
(2)
h+
=
(h+
),设3≤h1<h2≤2
,
则h2+
-h1-
=(h2-h1)(1-
)>0,l是h的增函数,
∴lmin=
×3+
=5
(米).(当h=3时取得最小值).
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
6
| ||
| h |
| ||
| 3 |
设外周长为l,则l=2AB+BC=
| 2h |
| sin60° |
6
| ||
| h |
| ||
| 3 |
| 3 |
6
| ||
| h |
| 2 |
当
| 3 |
6
| ||
| h |
| 6 |
| 2 |
| 6 |
(2)
| 3 |
6
| ||
| h |
| 3 |
| 6 |
| h |
| 3 |
则h2+
| 6 |
| h2 |
| 6 |
| h1 |
| 6 |
| h1h2 |
∴lmin=
| 3 |
6
| ||
| 3 |
| 3 |
点评:将实际问题转化为函数模型、利用基本不等式求函数的最值注意需满足:一正、二定、三相等;
利用函数单调性的定义判断函数的单调性、利用函数的单调性求函数的最值.
利用函数单调性的定义判断函数的单调性、利用函数的单调性求函数的最值.

练习册系列答案
相关题目
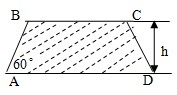 (2008•杨浦区二模)建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(2008•杨浦区二模)建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为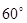 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为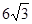 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段 与两腰长的和)要最小.
与两腰长的和)要最小.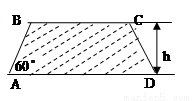
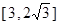 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?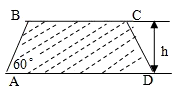 建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为 平 方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段BC与两腰长的和)要最小.
平 方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段BC与两腰长的和)要最小.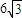 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段BC与两腰长的和)要最小.
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段BC与两腰长的和)要最小.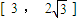 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?