题目内容
已知Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-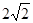 ),顶点C在
),顶点C在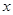 轴
轴
上。
(1)求BC边所在直线的方程;
(2)圆M为Rt△ABC外接圆,其中M为圆心,求圆M的方程;
(3)直线 与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面
与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面
积最小时的切线方程。
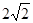 ),顶点C在
),顶点C在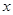 轴
轴上。
(1)求BC边所在直线的方程;
(2)圆M为Rt△ABC外接圆,其中M为圆心,求圆M的方程;
(3)直线
 与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面
与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程。
(1)因为AB所在的直线的斜率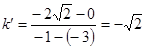 ,所以BC所在的直线的斜
,所以BC所在的直线的斜
率为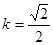 ,根据直线方程的点斜式,
,根据直线方程的点斜式,
BC所在的直线的方程为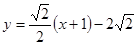 ,即
,即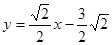 。
。
(2)由(1)可知,C点坐标为(3,0),又因为△ABC为以∠B为直角的直角三角形,
所以AC的中点即坐标原点是其外接圆圆心,所以外接圆方程为
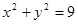 ;
;
(3)根据题意,设直线 的方程为
的方程为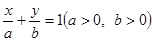 ,因为
,因为 与圆相切,所以
与圆相切,所以
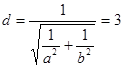
所以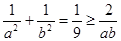 ,即
,即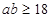 ,当且仅当
,当且仅当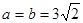 时取等。
时取等。
而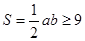 ,当且仅当
,当且仅当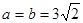 时取等。
时取等。
所以,三角形面积最小时切线方程是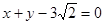 。
。
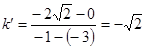 ,所以BC所在的直线的斜
,所以BC所在的直线的斜率为
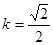 ,根据直线方程的点斜式,
,根据直线方程的点斜式,BC所在的直线的方程为
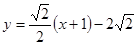 ,即
,即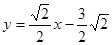 。
。(2)由(1)可知,C点坐标为(3,0),又因为△ABC为以∠B为直角的直角三角形,
所以AC的中点即坐标原点是其外接圆圆心,所以外接圆方程为
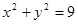 ;
;(3)根据题意,设直线
 的方程为
的方程为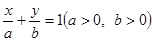 ,因为
,因为 与圆相切,所以
与圆相切,所以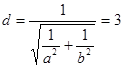
所以
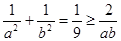 ,即
,即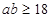 ,当且仅当
,当且仅当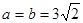 时取等。
时取等。而
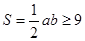 ,当且仅当
,当且仅当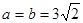 时取等。
时取等。所以,三角形面积最小时切线方程是
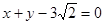 。
。略

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
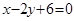 的斜率和它在
的斜率和它在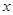 轴与
轴与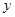 轴上的截距分别为( )
轴上的截距分别为( )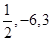
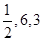
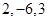
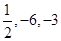
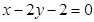 平行的直线方程是
平行的直线方程是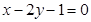
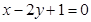
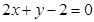
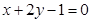
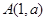 在直线
在直线 上,求经过点
上,求经过点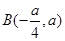 ,且与直线
,且与直线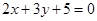 平行的直线的方程。
平行的直线的方程。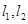 设原点到直线
设原点到直线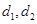 ,则
,则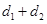 的最大值是 。
的最大值是 。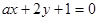 与直线
与直线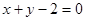 互相垂直,则实数a的值等于( )
互相垂直,则实数a的值等于( )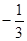
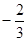
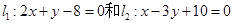 截得线段中点是M
截得线段中点是M