题目内容
已知集合A={a，
，1}，B={a2，a+b，0}，若A⊆B且B⊆A，则a=
| b | a |
-1
-1
，b=0
0
．分析：由题意若A⊆B且B⊆A，可得A=B，再根据集合相等的定义及集合的三要素进行求解；
解答：解：∵A⊆B且B⊆A，∴A=B，
∵集合A={a，
，1}，B={a2，a+b，0}，
∵分式
，所以a≠0，∴
=0，∴b=0，
∴集合A={a，0，1}，B={a2，a，0}，其中a≠1，否则不满足集合A的互异性，
∴a2=1，∴a=±1（1舍去），∴a=-1，
此时A={-1，0，1}，B={1，-1，0}，
故答案为：a=-1，b=0．
∵集合A={a，
| b |
| a |
∵分式
| b |
| a |
| b |
| a |
∴集合A={a，0，1}，B={a2，a，0}，其中a≠1，否则不满足集合A的互异性，
∴a2=1，∴a=±1（1舍去），∴a=-1，
此时A={-1，0，1}，B={1，-1，0}，
故答案为：a=-1，b=0．
点评：此题用到双包含来说明集合相等的概念，考查集合相等的定义及其三个性质，比较简单，注意集合的三个性质：确定性，互异性，无序性，此题是一道基础题．
练习册系列答案
口算题天天练系列答案
相关题目
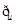B)＝R，则实数a的取值范围是 ( )