题目内容
平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H．若AE=3，BF=4，CG=5，则DH等于（ ）
分析：如图，过F点作CC1的垂线，过E点作DD1的垂线，垂足分别为N，M．由于平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H．得出四边形EFGH是平行四边形，从而有FG
EH，再结合△GFN≌△HEM，即可得出DH的长．
| ||
. |
解答：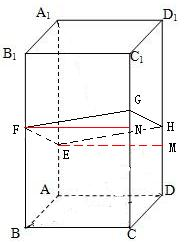
解：如图，过F点作CC1的垂线，过E点作DD1的垂线，垂足分别为N，M．
由于平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H．
∴四边形EFGH是平行四边形，
∴FG
EH，
又FN
EM，
∴△GFN≌△HEM，
∴GN=HM，而GN=CG-CN=CG-BF=5-4=1，
∴HM=1，
∴DH=DM+HM=AE+HM=3+1=4．
故选C．
解：如图，过F点作CC1的垂线，过E点作DD1的垂线，垂足分别为N，M．由于平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H．
∴四边形EFGH是平行四边形，
∴FG
| ||
. |
又FN
| ||
. |
∴△GFN≌△HEM，
∴GN=HM，而GN=CG-CN=CG-BF=5-4=1，
∴HM=1，
∴DH=DM+HM=AE+HM=3+1=4．
故选C．
点评：本小题主要考查棱柱的结构特征、三角形全等等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．
练习册系列答案
相关题目
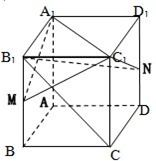如图，在正四棱柱ABCD-A1B1C1D1中，AB=a，AA1=2a，M、N分别是棱BB1，DD1的中点．
如图，在正四棱柱ABCD-A1B1C1D1中，AB=1，AA1=2，M、N分别为B1B和A1D的中点．