题目内容
已知等比数列{an} 的首项a1=2011,公比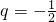 ,数列{an} 前n项和记为sn,前n项积记为
,数列{an} 前n项和记为sn,前n项积记为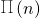
(1)证明s2≤sn≤s1
(2)判断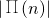 与
与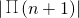 的大小,n为何值时,
的大小,n为何值时,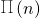 取得最大值
取得最大值
(3)证明{an} 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为d1,d2,d3,…dn,…,,证明:数列{dn}为等比数列.(参考数据210=1024)
解:(1)由等比数列{an} 的首项a1=2011,公比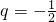 ,
,
得sn=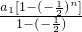 =
= a1[1-
a1[1- ],
],
①n是奇数时, =-
=- ,n=1时,-
,n=1时,- 最小,
最小,
②n是偶数时, =
= ,n=2时,
,n=2时, 最大,
最大,
综上:s2≤sn≤s1;
(2)∵|π(n)|=|a1a2a3…an|,∴ =|an+1|=2011×
=|an+1|=2011× ,
,
∵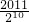 >1>
>1>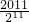 ,
,
当n≤10时,|π(n+1)|>|π(n)|;当n≥11时,|π(n+1)|<|π(n)|;
∴|π(n)|max=|π(11)|,但π(11)<0,∵π(10)<0,π(9)>0,π(12)>0,
∴π(n)的最大值是π(9)与π(12)中的较大者,
∵ =a10•a11•a12=
=a10•a11•a12= >1,
>1,
∴π(9)<π(12),
∴当n=12时,π(12)最大;
(3)对an,an+1,an+2进行调整,|an|随n增大而减小,{an}奇数项均为正,偶数项均为负,
①当n是奇数时,调整为:an+1,an+2,an;
则an+1+an=a1 +a1
+a1 =a1
=a1 ,2an+2=2a1
,2an+2=2a1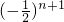 =a1
=a1 ,
,
∴an+1+an=2an+2,即an+1,an+2,an成等差数列;
②当n为偶数时,调整为:an,an+2,an+1,
则an+1+an=a1 +a1
+a1 =a1
=a1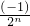 ,2an+2=2a1
,2an+2=2a1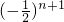 =a1
=a1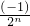 ,
,
∴an+1+an=2an+2,即an,an+2,an+1成等差数列;
所以{an}中的任意相邻三项按从小到大排列,总可以使其成等差数列.
①n是奇数时,公差dn=an+2-an+1=a1[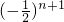 -
- ]=a1
]=a1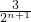 ;
;
②当n为偶数时,公差dn=an+2-an=a1[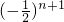 -
- ]=a1
]=a1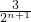 ,
,
无论n是奇数还是偶数,都有dn=a1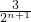 ,则
,则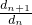 =
= ,
,
∴数列{dn}是以d1= a1,公比为
a1,公比为 的等比数列.
的等比数列.
分析:(1)由等比数列{an} 的首项和公比,利用等比数列的前n项和公式表示出数列{an} 前n项和sn,然后分n为奇数和偶数两种情况即可得到sn的最大值和最小值,得证;
(2)由π(n)表示前n项之积,表示出 ,根据n等于10时其值大于1,n等于11时其值小于1,得到|π(n)|最大值等于|π(11)|,但是π(11)小于0,而π(10)小于0,π(9)大于0,π(12)大于0,所以π(n)的最大值是π(9)与π(12)中的较大者,利用做商的方法即可判断出π(n)的最大值是π(12);
,根据n等于10时其值大于1,n等于11时其值小于1,得到|π(n)|最大值等于|π(11)|,但是π(11)小于0,而π(10)小于0,π(9)大于0,π(12)大于0,所以π(n)的最大值是π(9)与π(12)中的较大者,利用做商的方法即可判断出π(n)的最大值是π(12);
(3)设出数列{an} 中的任意相邻三项为:an,an+1,an+2,然后根据|an|随n增大而减小,{an}奇数项均为正,偶数项均为负,分n为奇数和偶数对设出的三项进行调整,利用等差数列的性质确定其三项为等差数列,并求出相应的公差,得到数列{dn}的通项,根据等比数列的性质可得数列{dn}为等比数列,得证.
点评:此题考查学生掌握确定数列为等差、等比数列的方法,灵活运用等比数列的前n项和公式及等比数列的性质化简求值,会利用做商的方法判断两式子的大小,是一道中档题.此题的逻辑性比较强,锻炼了学生的推理论证的能力.
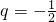 ,
,得sn=
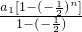 =
= a1[1-
a1[1- ],
],①n是奇数时,
 =-
=- ,n=1时,-
,n=1时,- 最小,
最小,②n是偶数时,
 =
= ,n=2时,
,n=2时, 最大,
最大,综上:s2≤sn≤s1;
(2)∵|π(n)|=|a1a2a3…an|,∴
 =|an+1|=2011×
=|an+1|=2011× ,
,∵
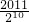 >1>
>1>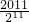 ,
,当n≤10时,|π(n+1)|>|π(n)|;当n≥11时,|π(n+1)|<|π(n)|;
∴|π(n)|max=|π(11)|,但π(11)<0,∵π(10)<0,π(9)>0,π(12)>0,
∴π(n)的最大值是π(9)与π(12)中的较大者,
∵
 =a10•a11•a12=
=a10•a11•a12= >1,
>1,∴π(9)<π(12),
∴当n=12时,π(12)最大;
(3)对an,an+1,an+2进行调整,|an|随n增大而减小,{an}奇数项均为正,偶数项均为负,
①当n是奇数时,调整为:an+1,an+2,an;
则an+1+an=a1
 +a1
+a1 =a1
=a1 ,2an+2=2a1
,2an+2=2a1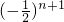 =a1
=a1 ,
,∴an+1+an=2an+2,即an+1,an+2,an成等差数列;
②当n为偶数时,调整为:an,an+2,an+1,
则an+1+an=a1
 +a1
+a1 =a1
=a1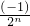 ,2an+2=2a1
,2an+2=2a1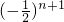 =a1
=a1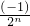 ,
,∴an+1+an=2an+2,即an,an+2,an+1成等差数列;
所以{an}中的任意相邻三项按从小到大排列,总可以使其成等差数列.
①n是奇数时,公差dn=an+2-an+1=a1[
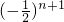 -
- ]=a1
]=a1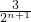 ;
;②当n为偶数时,公差dn=an+2-an=a1[
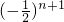 -
- ]=a1
]=a1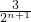 ,
,无论n是奇数还是偶数,都有dn=a1
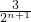 ,则
,则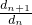 =
= ,
,∴数列{dn}是以d1=
 a1,公比为
a1,公比为 的等比数列.
的等比数列.分析:(1)由等比数列{an} 的首项和公比,利用等比数列的前n项和公式表示出数列{an} 前n项和sn,然后分n为奇数和偶数两种情况即可得到sn的最大值和最小值,得证;
(2)由π(n)表示前n项之积,表示出
 ,根据n等于10时其值大于1,n等于11时其值小于1,得到|π(n)|最大值等于|π(11)|,但是π(11)小于0,而π(10)小于0,π(9)大于0,π(12)大于0,所以π(n)的最大值是π(9)与π(12)中的较大者,利用做商的方法即可判断出π(n)的最大值是π(12);
,根据n等于10时其值大于1,n等于11时其值小于1,得到|π(n)|最大值等于|π(11)|,但是π(11)小于0,而π(10)小于0,π(9)大于0,π(12)大于0,所以π(n)的最大值是π(9)与π(12)中的较大者,利用做商的方法即可判断出π(n)的最大值是π(12);(3)设出数列{an} 中的任意相邻三项为:an,an+1,an+2,然后根据|an|随n增大而减小,{an}奇数项均为正,偶数项均为负,分n为奇数和偶数对设出的三项进行调整,利用等差数列的性质确定其三项为等差数列,并求出相应的公差,得到数列{dn}的通项,根据等比数列的性质可得数列{dn}为等比数列,得证.
点评:此题考查学生掌握确定数列为等差、等比数列的方法,灵活运用等比数列的前n项和公式及等比数列的性质化简求值,会利用做商的方法判断两式子的大小,是一道中档题.此题的逻辑性比较强,锻炼了学生的推理论证的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目