题目内容
如图,设F是椭圆:C:
+
=1(a>b>0)的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.
(1)求椭圆C的标准方程;
(2)若过点P的直线与椭圆相交于不同两点A,B,求证:∠AFM=∠BFN;
(3)(理)求三角形ABF面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的标准方程;
(2)若过点P的直线与椭圆相交于不同两点A,B,求证:∠AFM=∠BFN;
(3)(理)求三角形ABF面积的最大值.
(1)∵线段MN为椭圆的长轴,且|MN|=8,∴a=4
∵|PM|=2|MF|,
∴
-a=2(a-c)
∴a2-ac=2ac-2c2,
∴2e2-3e+1=0,
解得e=
或e=1(舍去)
∴c=2,b2=a2-c2=12,
∴椭圆的标准方程为
+
=1.
(2)当AB的斜率为0时,显然∠AFM=∠BFM=0,满足题意.
当AB方程为x=my-8,代入椭圆方程整理得
(3m2+4)y2-48my+144=0,
设A(x1,y1),B(x2,y2),
则y1+y2=
,y1y2=
,
∴KAF+KBF=
+
=
+
=
=
=0
∴KAF+KBF=0,从而∠AFM=∠BFN 综上可知,恒有∠AFM=∠BFN.
(3)(理)∵P(-8,0),F(-2,0),∴|PF|=6,
∴|y2-y1|=
=
=
,
∴S△ABF=S△PBF-S△PAF
=
|PF|•|y2|-
|PF|•|y1|
=
|PF|•|y2-y1|
=
=
=
≤
=3
当且仅当3
=
即m2=
(此时适合△>0的条件)时取等号
∴三角形ABF面积的最大值是3
.
∵|PM|=2|MF|,
∴
| a2 |
| c |
∴a2-ac=2ac-2c2,
∴2e2-3e+1=0,
解得e=
| 1 |
| 2 |
∴c=2,b2=a2-c2=12,
∴椭圆的标准方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)当AB的斜率为0时,显然∠AFM=∠BFM=0,满足题意.
当AB方程为x=my-8,代入椭圆方程整理得
(3m2+4)y2-48my+144=0,
设A(x1,y1),B(x2,y2),
则y1+y2=
| 48m |
| 3m2+4 |
| 144 |
| 3m2+4 |
∴KAF+KBF=
| y1 |
| x1+2 |
| y2 |
| x2+2 |
| y1 |
| m1-6 |
| y2 |
| my2-6 |
=
| 2my1y2-6(y1+y2) | ||
(my1-6)(m
|
=
| ||||
| (my1-6)(my2-6) |
∴KAF+KBF=0,从而∠AFM=∠BFN 综上可知,恒有∠AFM=∠BFN.
(3)(理)∵P(-8,0),F(-2,0),∴|PF|=6,
∴|y2-y1|=
| (y1+y2)2-4y1y2 |
=
(
|
=
24
| ||
| 3m2+4 |
∴S△ABF=S△PBF-S△PAF
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
72
| ||
| 3m2+4 |
72
| ||
| 3(m2-4)+16 |
=
| 72 | ||||||
3
|
≤
| 72 | ||
2
|
| 3 |
当且仅当3
| m2-4 |
| 16 | ||
|
即m2=
| 28 |
| 3 |
∴三角形ABF面积的最大值是3
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a>b>0)的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.
(a>b>0)的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.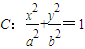 (a>b>0)的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.
(a>b>0)的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.