题目内容
(本题满分12分)如图,在四棱锥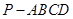 中,底面
中,底面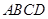 为平行四边形,
为平行四边形,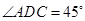 ,
,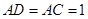 ,
,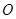 为
为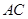 中点,
中点,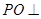 平面
平面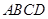 ,
, 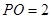 ,
,
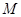 为
为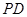 中点.
中点.

(1)证明: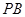 //平面
//平面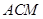 ;
;
(2)证明: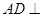 平面
平面 ;
;
(3)求直线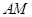 与平面
与平面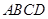 所成角的正切值.
所成角的正切值.
【答案】
(1)先证PB//MO,再利用线面平行的判定定理即可证明;
(2)分别证明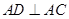 ,
,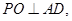
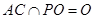 ,根据线面垂直的判定定理可证;(3)
,根据线面垂直的判定定理可证;(3)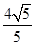
【解析】
试题分析:(1)连接BD,MO,在平行四边形ABCD中,
因为O为AC的中点,所以O为BD的中点,
又M为PD的中点,所以PB//MO。 ……2分
因为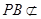 平面ACM,
平面ACM,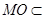 平面ACM,所以PB//平面ACM。 ……4分
平面ACM,所以PB//平面ACM。 ……4分
(2)因为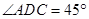 ,且AD=AC=1,所以
,且AD=AC=1,所以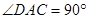 ,即
,即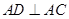 , ……6分
, ……6分
又PO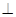 平面ABCD,
平面ABCD,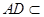 平面ABCD,所以
平面ABCD,所以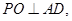
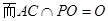 ,所以
,所以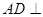 平面PAC。 ……8分
平面PAC。 ……8分
(3)取DO中点N,连接MN,AN,因为M为PD的中点,所以MN//PO,
且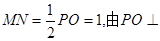 平面ABCD,得
平面ABCD,得 平面ABCD,
平面ABCD,
所以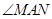 是直线AM与平面ABCD所成的角, ……10分
是直线AM与平面ABCD所成的角, ……10分
在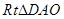 中,
中,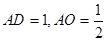 ,所以
,所以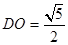 ,
,
从而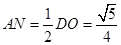 ,
,
在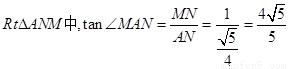 ,
,
即直线AM与平面ABCD所成角的正切值为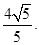 ……12分
……12分
考点:本小题主要考查空间中线面平行和线面垂直的证明以及线面角的求解,考查学生的空间想象能力和推理论证能力以及运算求解能力.
点评:在空间中证明直线、平面之间的位置关系时要严格按照判定定理和性质定理进行,定理中要求的条件缺一不可.

练习册系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
