题目内容
已知{an}是递减的等差数列，若a4•a6=775，a2+a8=56，则前 项和最大．
【答案】分析：根据等差数列的性质可得 a4•a6=775，a4 +a6 =56，求出a4 和 a6 的值，即可得到公差d的值，进而得到
通项公式 an=43-3n，由题意知所有的正项的和最大，由an≥0 可得n≤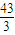
，故前14项的和最大．
解答：解：根据等差数列的性质可得 a4•a6=775，a4 +a6 =56，∴a4 =31，a6=25．
∴公差d=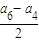
=-3，∴an=31+（n-4）d=43-3n．
由an≥0 可得n≤
，故前14项的和最大，
故答案为：14．
点评：本题考查等差数列的定义和性质，通项公式，求出通项公式 an=43-3n，是解题的关键．
通项公式 an=43-3n，由题意知所有的正项的和最大，由an≥0 可得n≤
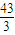，故前14项的和最大．解答：解：根据等差数列的性质可得 a4•a6=775，a4 +a6 =56，∴a4 =31，a6=25．
∴公差d=
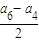=-3，∴an=31+（n-4）d=43-3n．由an≥0 可得n≤
，故前14项的和最大，故答案为：14．
点评：本题考查等差数列的定义和性质，通项公式，求出通项公式 an=43-3n，是解题的关键．
练习册系列答案
相关题目
已知{an}是递减等比数列，a2=2，a1+a3=5，则a1a2+a2a3+…+anan+1（n∈N*）的取值范围是（ ）
| A、[12，16） | ||||
| B、[8，16） | ||||
C、[8，
| ||||
D、[
|