题目内容
抛掷一个均匀的正方体玩具（各面分别标有数字1、2、3、4、5、6），事件A表示“朝上一面的数是奇数”，事件B表示“朝上一面的数不超过3”，求P（A+B）.
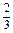
方法一 因为A+B的意义是事件A发生或事件B发生，所以一次试验中只要出现1、2、3、5四个可能结果之一时，A+B就发生，而一次试验的所有可能结果为6个，所以P（A+B）=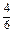
=.
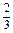方法二 记事件C为“朝上一面的数为2”，
则A+B=A+C，且A与C互斥.
又因为P（C）=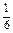
，P（A）=
，
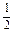所以P（A+B）=P（A+C）=P（A）+P（C）
=+=.
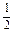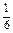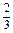方法三 记事件D为“朝上一面的数为4或6”，则事件D发生时，事件A和事件B都不发生，即事件A+B不发生.又事件A+B发生即事件A发生或事件B发生时，事件D不发生，所以事件A+B与事件D为对立事件.
因为P（D）=
=
，
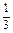所以P（A+B）=1-P（D）=1-=.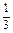
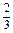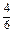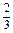=.方法二 记事件C为“朝上一面的数为2”，
则A+B=A+C，且A与C互斥.
又因为P（C）=
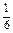，P（A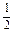）=，所以P（A+B）=P（A+C）=P（A）+P（C）
=
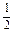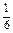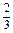+=.方法三 记事件D为“朝上一面的数为4或6”，则事件D发生时，事件A和事件B都不发生，即事件A+B不发生.又事件A+B发生即事件A发生或事件B发生时，事件D不发生，所以事件A+B与事件D为对立事件.
因为P（D）=
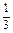=，所以P（A+B）=1-P（D）=1-
=.
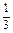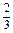练习册系列答案
相关题目
内部作一条射线
，与线段
交与点
，则
的概率是 .
（各学校是否录取他相互独立，允许他可以被多个学校同时录取）.
B．
C．
D．