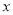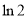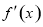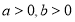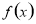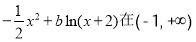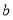题目内容
设a为实数,函数f(x)=ex-2x+2a,x∈R.
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2-1且x >0时,ex >x2-2ax+1
(1) 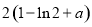 (2)见解析
(2)见解析
【解析】
试题分析:(1)首先求出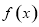 的导数
的导数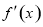 ,解方程
,解方程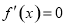 ,进一步得到不等式
,进一步得到不等式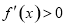 与
与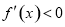 的解集,从而得到函数的单调区间和极值.
的解集,从而得到函数的单调区间和极值.
(2)欲证当a>ln2-1且x >0时,ex >x2-2ax+1,
令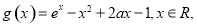
则只需证当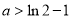 时,
时,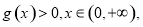
从而转化为利用导数求 的最小值问题.
的最小值问题.
试题解析:【解析】
(1)由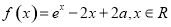 知
知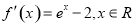
令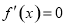 得
得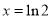 于是当
于是当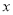 变化时,
变化时,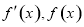 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| - | 0 | + |
| 单调递减 |
| 单调递增 |
故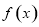 的单调递减区间是
的单调递减区间是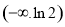 ,间调递增区间是
,间调递增区间是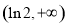
在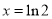 处取得极小值,极小值为
处取得极小值,极小值为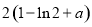 6分
6分
(2)设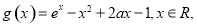 ,于是
,于是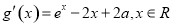
由(1)知,当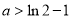 时,
时,
 最小值为
最小值为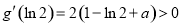
于是对任意的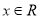 ,都有
,都有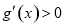 ,所以
,所以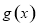 在
在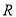 内单调递增.
内单调递增.
于是当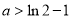 时,对任意
时,对任意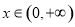
都有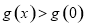
而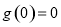 ,从而对任意
,从而对任意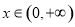 ,
,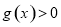
即: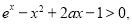 故,
故,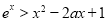 14分
14分
考点:1、导数在研究函数性质中的应用;2、等价转论的思想.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目