题目内容
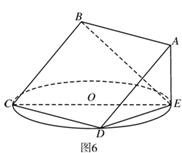
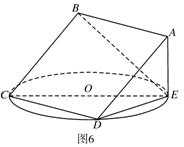
(本题12分) 如图,正方形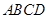 所在平面与圆
所在平面与圆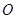 所在平面相交于
所在平面相交于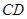 ,线段
,线段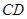 为圆
为圆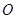 的弦,
的弦,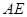 垂直于圆
垂直于圆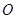 所在平面,垂足
所在平面,垂足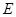 是圆
是圆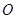 上异于
上异于 、
、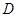 的点,
的点,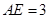 ,圆
,圆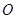 的直径为9.
的直径为9.
(1)求证:平面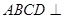 平面
平面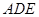 ;
;
(2)求正方形的边长;
(3)求二面角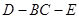 的平面角的正切值.
的平面角的正切值.
【答案】
(1)略
(2)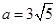
(3)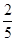
【解析】(1)证明:∵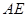 垂直于圆
垂直于圆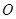 所在平面,
所在平面,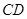 在圆
在圆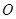 所在平面上,
所在平面上,
∴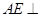
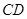 .
.
在正方形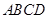 中,
中,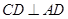 ,
,
∵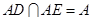 ,∴
,∴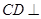 平面
平面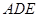 .
.
∵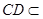 平面
平面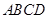 ,
,
∴平面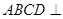 平面
平面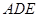 . ……… 4分
. ……… 4分
(2)∵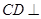 平面
平面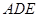 ,
,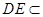 平面
平面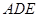 ,
,
∴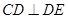 .
.
∴ 为圆
为圆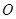 的直径,即
的直径,即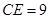 .
.
设正方形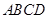 的边长为
的边长为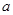 ,
,
在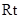 △
△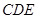 中,
中,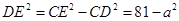 ,
,
在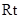 △
△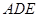 中,
中,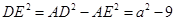 ,
,
由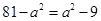 ,解得,
,解得,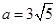 .
……… 8分
.
……… 8分
(3). 过点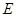 作
作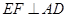 于点
于点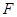 ,作
,作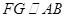 交
交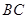 于点
于点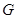 ,连结
,连结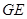 ,
,
由于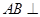 平面
平面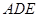 ,
,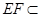 平面
平面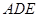 ,
,
∴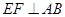 .∵
.∵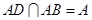 ,
,
∴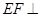 平面
平面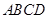 .∵
.∵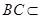 平面
平面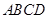 ,∴
,∴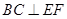 .
.
∵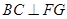 ,
,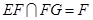 ,∴
,∴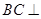 平面
平面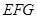 .
.
∵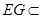 平面
平面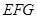 ,∴
,∴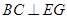 .
.
∴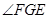 是二面角
是二面角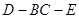 的平面角.
……………… 10分
的平面角.
……………… 10分
在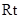 △
△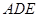 中,
中,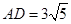 ,
,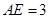 ,
,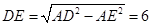
∵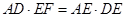 ,∴
,∴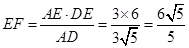 .
.
在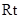 △
△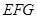 中,
中,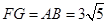 , ∴
, ∴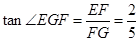 .
.
故二面角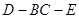 的平面角的正切值为
的平面角的正切值为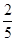 . ………………12分
. ………………12分

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
 中,
中,  ,点
,点 是棱
是棱 上一点.
上一点.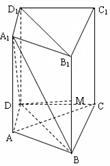
 面
面 ;
; ;
; 中,
中,  ,点
,点 是棱
是棱 上一点
上一点 面
面 ;
; ;
;
 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.