题目内容
已知向量 =(cosθ,sinθ),
=(cosθ,sinθ), =(cos2θ,sin2θ),
=(cos2θ,sin2θ), =(-1,0),
=(-1,0), =(0,1).
=(0,1).
(1)求证: ⊥(
⊥( +
+ ) (其中θ≠kπ);
) (其中θ≠kπ);
(2)设f(θ)= •(
•( -
- ),且θ∈(0,π),求f(θ)的值域.
),且θ∈(0,π),求f(θ)的值域.
解(1)∵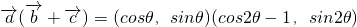 =cosθcos2θ+sinθsin2θ-cosθ
=cosθcos2θ+sinθsin2θ-cosθ
=cos(2θ-θ)-cosθ=0,
∴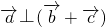
(2)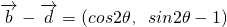
f(θ)=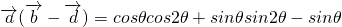
=cosθ-sinθ=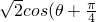 )
)
∵θ∈(0,π),
∴θ+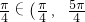 ),
),
∴cos(θ+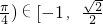 )
)
∴f(θ)的值域为[- ,1)
,1)
分析:(1)利用向量的数量积公式求出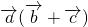 ,利用向量垂直的常用条件得到证明.
,利用向量垂直的常用条件得到证明.
(2)利用向量的数量积公式求出f(θ),将f(θ)化简,利用三角函数的有界性求出其值域.
点评:平面向量与三角函数的结合的试题中,向量一般都是转化的工具,然后利用三角函数的公式及性质进行求解,正弦定理与余弦定理是用来解三角形的常用工具,还考查了基本不等式在求最值中的应用.
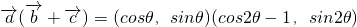 =cosθcos2θ+sinθsin2θ-cosθ
=cosθcos2θ+sinθsin2θ-cosθ=cos(2θ-θ)-cosθ=0,
∴
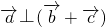
(2)
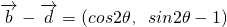
f(θ)=
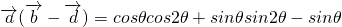
=cosθ-sinθ=
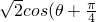 )
)∵θ∈(0,π),
∴θ+
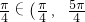 ),
),∴cos(θ+
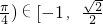 )
)
∴f(θ)的值域为[-
 ,1)
,1)分析:(1)利用向量的数量积公式求出
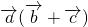 ,利用向量垂直的常用条件得到证明.
,利用向量垂直的常用条件得到证明.(2)利用向量的数量积公式求出f(θ),将f(θ)化简,利用三角函数的有界性求出其值域.
点评:平面向量与三角函数的结合的试题中,向量一般都是转化的工具,然后利用三角函数的公式及性质进行求解,正弦定理与余弦定理是用来解三角形的常用工具,还考查了基本不等式在求最值中的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |