题目内容
给出下列四个命题:①如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题;
②已知向量
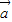 ,
,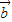 满足
满足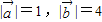 ,且
,且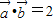 ,则
,则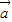 与
与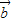 的夹角为
的夹角为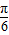 ;
;③若函数f(x+1)是奇函数,f(x-1)是偶函数,且f(0)=2,则f(2012)=2;
④已知函数
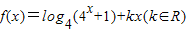 是偶函数,函数
是偶函数,函数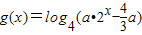 ,若函数f(x)的图象与函数g(x)的图象有且只有一个公共点,则实数a的取值范围是(1,+∞).
,若函数f(x)的图象与函数g(x)的图象有且只有一个公共点,则实数a的取值范围是(1,+∞).其中正确命题的序号为 .
【答案】分析:根据复合命题真假性的真值表,可判断出命题“p”为假命题,进而命题“q”是真命题,可判断(1);
根据向量夹角公式,结合已知求出两个向量的夹角,可判断(2);
根据已知,结合函数奇偶性的定义,分析出函数的周期性,进而求出f(2012)的值,可判断(3);
根据函数奇偶性的定义,求出k值,进而根据函数f(x)的图象与函数g(x)的图象有且只有一个公共点,求出实数a的取值范围,可判断(4).
解答:解:若命题“¬p”与命题“p或q”都是真命题,则命题“p”为假命题,命题“q”是真命题,故①正确;
若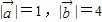 ,且
,且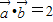 ,则
,则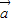 与
与 的夹角θ满足,cosθ=
的夹角θ满足,cosθ=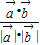 =
= ,则
,则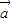 与
与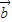 的夹角为
的夹角为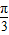 ,故②错误;
,故②错误;
若函数f(x+1)是奇函数,f(x+1)=-f(-x+1),若f(x-1)是偶函数,则f(x-1)=f(-x-1)
故f(x+4)=f(x+3+1)=-f[-(x+3)+1]=-f(-x-2)=-f[-(x+1)-1]=-f(x+1-1)=-f(x)
则f(x+8)=-f(x+4)=f(x),即函数f(x)的周期为8,由f(0)=2,则f(2012)=f(4)=-2,故③错误;
由f(x)为偶函数,故log4(4-x+1)-kx=log4(4x+1)+kx对所有x∈R都成立,即(2k+1)x=0对所有x∈R都成立,故k=- .
.
由方程log4(4x+1)- x=
x=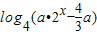 (*)
(*)
可变形为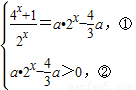 ,由②得
,由②得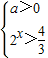 或
或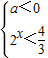 ,
,
令2x=t,则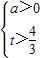 ,或
,或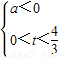
由①得(a-1)(2x)2- a•2x-1=0,设h(t)=(a-1)t2-
a•2x-1=0,设h(t)=(a-1)t2- at-1
at-1
∴当a>0时,(a-1)h( )<0⇒a>1,
)<0⇒a>1,
当a<0时,h(0)=-1<0,h( )>0⇒a不存在,
)>0⇒a不存在,
当△=(- a)2+4(a-1)=0时,a=
a)2+4(a-1)=0时,a= 或a=-3,
或a=-3,
若a= ,则t=-2,不合题意,舍去,若a=-3,则t=
,则t=-2,不合题意,舍去,若a=-3,则t= ,满足题意,
,满足题意,
∴当a=-3或a>1时,函数f(x)与g(x)的图象有且只有一个公共点,故④错误
故答案为:①
点评:本题以命题的真假判断为载体考查了函数的奇偶性与周期性,复合命题,向量夹角公式等知识点,其中(3)(4)是函数图象和性质的综合应用,难度非常大.
根据向量夹角公式,结合已知求出两个向量的夹角,可判断(2);
根据已知,结合函数奇偶性的定义,分析出函数的周期性,进而求出f(2012)的值,可判断(3);
根据函数奇偶性的定义,求出k值,进而根据函数f(x)的图象与函数g(x)的图象有且只有一个公共点,求出实数a的取值范围,可判断(4).
解答:解:若命题“¬p”与命题“p或q”都是真命题,则命题“p”为假命题,命题“q”是真命题,故①正确;
若
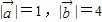 ,且
,且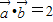 ,则
,则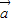 与
与 的夹角θ满足,cosθ=
的夹角θ满足,cosθ=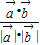 =
= ,则
,则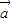 与
与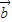 的夹角为
的夹角为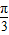 ,故②错误;
,故②错误;若函数f(x+1)是奇函数,f(x+1)=-f(-x+1),若f(x-1)是偶函数,则f(x-1)=f(-x-1)
故f(x+4)=f(x+3+1)=-f[-(x+3)+1]=-f(-x-2)=-f[-(x+1)-1]=-f(x+1-1)=-f(x)
则f(x+8)=-f(x+4)=f(x),即函数f(x)的周期为8,由f(0)=2,则f(2012)=f(4)=-2,故③错误;
由f(x)为偶函数,故log4(4-x+1)-kx=log4(4x+1)+kx对所有x∈R都成立,即(2k+1)x=0对所有x∈R都成立,故k=-
 .
.由方程log4(4x+1)-
 x=
x=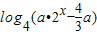 (*)
(*)可变形为
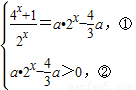 ,由②得
,由②得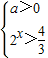 或
或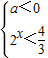 ,
,令2x=t,则
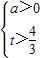 ,或
,或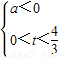
由①得(a-1)(2x)2-
 a•2x-1=0,设h(t)=(a-1)t2-
a•2x-1=0,设h(t)=(a-1)t2- at-1
at-1∴当a>0时,(a-1)h(
 )<0⇒a>1,
)<0⇒a>1,当a<0时,h(0)=-1<0,h(
 )>0⇒a不存在,
)>0⇒a不存在,当△=(-
 a)2+4(a-1)=0时,a=
a)2+4(a-1)=0时,a= 或a=-3,
或a=-3,若a=
 ,则t=-2,不合题意,舍去,若a=-3,则t=
,则t=-2,不合题意,舍去,若a=-3,则t= ,满足题意,
,满足题意,∴当a=-3或a>1时,函数f(x)与g(x)的图象有且只有一个公共点,故④错误
故答案为:①
点评:本题以命题的真假判断为载体考查了函数的奇偶性与周期性,复合命题,向量夹角公式等知识点,其中(3)(4)是函数图象和性质的综合应用,难度非常大.

练习册系列答案
相关题目