题目内容
(本题10分)已知函数![]() 有极值.
有极值.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 在
在![]() 处取得极值,且当
处取得极值,且当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(1)![]()
(2)![]()
解析:
(1)∵![]() ,∴
,∴![]()
要使![]() 有极值,则方程
有极值,则方程![]() 有两个实数解,
有两个实数解,
从而△=![]() ,∴
,∴![]() .
.
(2)∵![]() 在
在![]() 处取得极值,
处取得极值,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() ,函数单调递增,
,函数单调递增,
当![]()
![]() 时,
时,![]() ,函数单调递减.
,函数单调递减.
∴![]() 时,
时,![]() 在
在![]() 处取得最大值
处取得最大值![]() ,
,
∵![]() 时,
时,![]() 恒成立,
恒成立,
∴![]()
![]() ,即
,即![]() ,
,
∴![]() 或
或![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
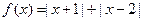 .
.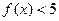 成立,求实数
成立,求实数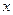 的取值范围;
的取值范围;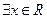 满足不等式
满足不等式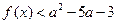 ,求实数
,求实数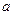 取值范围.
取值范围. (
( ∈R).
∈R).
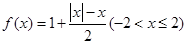
 (
( 是自然对数的底数,
是自然对数的底数, ).
). ,不等式
,不等式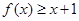 恒成立;
恒成立; 的前
的前 项和为
项和为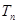 ,求证:
,求证: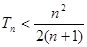 .
.