题目内容
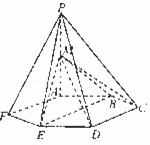
如图,六棱锥P-ABCDEF的底面ABCDEF是边长为l的正六边形,顶点P在底面上的射影是BF的中点O.(1)求证:PA⊥BF;
(2)若直线PB与平面ABCDEF所成的角为
 ,求二面角A-PB-D的余弦值.
,求二面角A-PB-D的余弦值.
【答案】分析:(1)利用线面垂直证明线线垂直,即证明BF⊥平面PAO;
(2)以OB,OD,OP分别为x,y,z轴,建立空间直角坐标系,用坐标表示点,用坐标表示向量,进而求出两平面的法向量,利用向量的夹角公式可求二面角A-PB-D的余弦值.
解答: (1)证明:连接OA,则∵AB=AF,BF的中点O,∴AO⊥BF
(1)证明:连接OA,则∵AB=AF,BF的中点O,∴AO⊥BF
∵顶点P在底面上的射影是BF的中点O
∴PO⊥BF
∵AO∩PO=O
∴BF⊥平面PAO
∵PA?平面PAO
∴PA⊥BF;
(2)解:∵顶点P在底面上的射影是BF的中点O
∴∠PBO为直线PB与平面ABCDEF所成的角
∵直线PB与平面ABCDEF所成的角为 ,
,
∴∠PBO=
以OB,OD,OP分别为x,y,z轴,建立空间直角坐标系,则A(0,- ,0),B(
,0),B( ,0,0),P(0,0,
,0,0),P(0,0, ),D(0,
),D(0, ,0)
,0)
∴ ,
, ,
,
设平面APB的法向量为 ,则
,则 ,
,
∴ ,领z=-1,可得
,领z=-1,可得
同理可得平面DPB的法向量为
设二面角A-PB-D的平面角为α,则
点评:本题考查线线垂直,考查面面角,解题的关键是利用线面垂直证明线线垂直,利用向量法,求面面角,属于中档题.
(2)以OB,OD,OP分别为x,y,z轴,建立空间直角坐标系,用坐标表示点,用坐标表示向量,进而求出两平面的法向量,利用向量的夹角公式可求二面角A-PB-D的余弦值.
解答:
 (1)证明:连接OA,则∵AB=AF,BF的中点O,∴AO⊥BF
(1)证明:连接OA,则∵AB=AF,BF的中点O,∴AO⊥BF∵顶点P在底面上的射影是BF的中点O
∴PO⊥BF
∵AO∩PO=O
∴BF⊥平面PAO
∵PA?平面PAO
∴PA⊥BF;
(2)解:∵顶点P在底面上的射影是BF的中点O
∴∠PBO为直线PB与平面ABCDEF所成的角
∵直线PB与平面ABCDEF所成的角为
 ,
,∴∠PBO=

以OB,OD,OP分别为x,y,z轴,建立空间直角坐标系,则A(0,-
 ,0),B(
,0),B( ,0,0),P(0,0,
,0,0),P(0,0, ),D(0,
),D(0, ,0)
,0)∴
 ,
, ,
,
设平面APB的法向量为
 ,则
,则 ,
,∴
 ,领z=-1,可得
,领z=-1,可得
同理可得平面DPB的法向量为

设二面角A-PB-D的平面角为α,则

点评:本题考查线线垂直,考查面面角,解题的关键是利用线面垂直证明线线垂直,利用向量法,求面面角,属于中档题.

练习册系列答案
相关题目


 ,M是PA的中点.
,M是PA的中点.
 ,M是PA的中点.
,M是PA的中点.