题目内容
已知过原点的直线与圆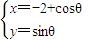 (其中θ为参数)相切,若切点在第二象限,则该直线的方程为 .
(其中θ为参数)相切,若切点在第二象限,则该直线的方程为 .
【答案】分析:由题意圆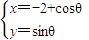 (其中θ为参数)将圆C先化为一般方程坐标,然后再利用相切计算直线的方程.
(其中θ为参数)将圆C先化为一般方程坐标,然后再利用相切计算直线的方程.
解答:解:∵圆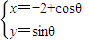 (其中θ为参数)相切,
(其中θ为参数)相切,
∴(x+2)2+y2=1,圆心为(-2,0),半径r=1,
∵过原点的直线可设y=kx,
∵过原点的直线与圆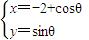 (其中θ为参数)相切,
(其中θ为参数)相切,
∴1=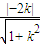 ,
,
∴k=±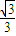 ,∵切点在第二象限,
,∵切点在第二象限,
∴k=-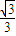 ,
,
∴y=-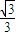 x,
x,
故答案为:y=-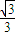 x.
x.
点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.
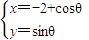 (其中θ为参数)将圆C先化为一般方程坐标,然后再利用相切计算直线的方程.
(其中θ为参数)将圆C先化为一般方程坐标,然后再利用相切计算直线的方程.解答:解:∵圆
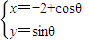 (其中θ为参数)相切,
(其中θ为参数)相切,∴(x+2)2+y2=1,圆心为(-2,0),半径r=1,
∵过原点的直线可设y=kx,
∵过原点的直线与圆
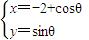 (其中θ为参数)相切,
(其中θ为参数)相切,∴1=
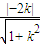 ,
,∴k=±
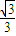 ,∵切点在第二象限,
,∵切点在第二象限,∴k=-
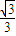 ,
,∴y=-
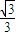 x,
x,故答案为:y=-
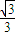 x.
x.点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目

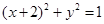 相切,若切点在第二象限,则该直线的方程为 .
相切,若切点在第二象限,则该直线的方程为 .