Question

平行四边形ABCD中，·=0，沿BD折成直二面角A一BD－C，且4AB² +2BD² =1，则三棱锥A－BCD的外接球的表面积为（   ）

A．

B．

C．

D．

Answer 1

A

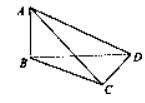
试题分析：根据题意，可知折叠后的三棱锥如右图所示．
∵·=0，∴∠ABD=∠CBD=90°，
由此可得AC的中点O即为外接球的球心,
又∵二面角A-BD-C是直二面角，即平面ABD⊥平面BCD，且AB⊥BD,
∴AB⊥平面BCD，可得△ABC是以AC为斜边的直角三角形
∵
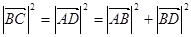
∴R t△ABC中， 
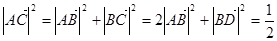
从而三棱锥A-BCD的外接球的表面积 
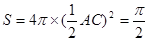
故答案为：A
点评：本题将平行四边折叠，求折成三棱锥的外接球表面积，着重考查了面面垂直的性质、球表面积公式和球内接多面体的性质等知识，属于中档题．