Question

已知f（x）=2x²+bx+c，不等式f（x）＜0的解集是（0，5）．
（1）．求f（x）的解析式；
（2）．已知g（x）=f（x）+mx-6，求当m为何值时，g（x）为偶函数．
（3）．若g（x）=f（x）+mx-6在[1，2]上最小值为h（m），试讨论h（m）-k=0的零点个数．（k为常数）．

Answer 1

分析：（1）由题意可知f（x）=2x²+bx+c=0的解为0，5，根据方程的根与系数关系可求b，c，进而可求f（x）
（2）由g（x）为偶函数，则对称轴为x=0，可求m
（3）由g（x）=f（x）+mx-6=2x²+（m-10）x-6，对称轴是x=

10-m

4

，要求最小值，需要讨论对称轴与区间[1，2]的位置关系：分①当

10-m

4

＜1，②当1≤

10-m

4

≤2，③当

10-m

4

＞2，分别求解，而h（m）-k=0根的个数等价于函数y=h（m）与y=k两个图象公共点的个数，结合函数的图象可求

解答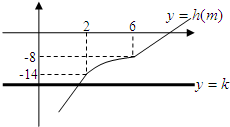：解：（1）由不等式f（x）＜0的解集为（0，5）可知，f（x）=2x²+bx+c=0的解为0，5
根据方程的根与系数关系可得c=0，5=-

b

2

即b=-10，c=0
∴f（x）=2x²-10x．
（2）∵g（x）=f（x）+mx-6=2x²+（m-10）x-6，对称轴是x=

m-10

4

．
若使得g（x）为偶函数，则对称轴为x=0
∴m=10
（3）∵g（x）=f（x）+mx-6=2x²+（m-10）x-6，对称轴是x=

10-m

4

①当

10-m

4

＜1，即m＞6时，y=g（x）在x∈[1，2]上单调增，故h（m）=g（1）=m-14；
②当1≤

10-m

4

≤2，即2≤m≤6时，y=g（x）在x∈[1，2]先减后增，于是h(m)=g(

m-10

4

)=-

m2

8

+

5

2

m-

37

2

③当

10-m

4

＞2，即m＜2时，y=g（x）在x∈[1，2]上单调减，故h（m）=g（2）=2m-18．
综上所述，h(m)=

m-14(m＞6) - m2 8 + 5 2 m- 37 2 (2≤m≤6) 2m-18(m＜2)

（3）由题知，h（m）-k=0根的个数等价于函数y=h（m）与y=k两个图象公共点的个数，
由y=h（m）的解析式，可知y=h（m）在R上单调递增，
结合图象知，不论k为何值，方程h（m）-k=0总在在唯一的实数根．

点评：本题主要考查了利用二次方程与二次不等式的关系求解函数解析式及二次函数在闭区间上的最值的求解，方程的根与函数的零点的相互转化，体现了转化思想及数形结合思想的应用