题目内容
有8人排成一排照相,要求A、B两人不相邻,C,D,E三人互不相邻,则不同的排法有( )
| A.11520 | B.8640 | C.5640 | D.2880 |
分三类:第一类:先排没有限制条件的3人(设为F、G、H),有
种,再用“插空法”排A、B、C,有
种,最后用“插空法”排A、B,有
种,∴第一类共有
•
•
=6 048种排法.
第二类:先排没有限制条件的3人(设为F、G、H),有
种,再将C,D,E中选两个捆在一起有
种捆法,把捆在一起的两人看作一人和另外一人用“插空法”排在四个空隙中,有
种排法,然后从D、E中选一个放在捆在一起的两元素之间有
种方法,最后一个元素安排在剩余的6个空隙中有
种方法,故第二类共有
•
•
•
•
=5 184种排法.
第三类:先排没有限制条件的3人(设为F、G、H),有
种排法,再把C,D,E三个人“捆绑”在一起有
种“捆法”,看作一个元素安排在四个空隙中,有
种放法,然后再把A、B利用“插空法”安排在C,D,E之间的两个空隙中,有
种方法,故第三类共有
•
•
•
=288种方法.
综上所述,符合条件的所有排法共有6 048+5 184+288=11520种.
故选A.
| A | 33 |
| A | 34 |
| A | 27 |
| A | 33 |
| A | 34 |
| A | 27 |
第二类:先排没有限制条件的3人(设为F、G、H),有
| A | 33 |
| A | 23 |
| A | 24 |
| A | 12 |
| A | 16 |
| A | 33 |
| A | 23 |
| A | 24 |
| A | 12 |
| A | 16 |
第三类:先排没有限制条件的3人(设为F、G、H),有
| A | 33 |
| A | 33 |
| A | 14 |
| A | 22 |
| A | 33 |
| A | 33 |
| A | 14 |
| A | 22 |
综上所述,符合条件的所有排法共有6 048+5 184+288=11520种.
故选A.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
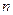 的最小值,使得存在以红点为顶点的
的最小值,使得存在以红点为顶点的