题目内容
圆x2+y2=9的动弦AB垂直于x轴,P 为AB上的点,且︱AP︱·︱BP︱=4,(1)求点P的轨迹;(2)若M(x,y)是(1)中曲线上任一点,求t= 的取值范围。
的取值范围。
【答案】
解:(1)∵弦AB垂直于x轴,∴xA=xB,yA=-yB∴设A(x,y1),B(x,-y1),P(x,y)
∵︱AP︱·︱BP︱=4,∴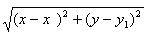 ·
·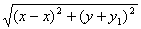 =4
=4
即︱y-y1︱·︱y+y1︱=4 ∴︱y2-y12︱=4
∵A(x,y1)在圆上,∴y12=9-x2
∴︱ x2+ y2-9︱=4
∵P(x,y)在圆内,∴x2+ y2<9
∴9-(x2+ y2)=4
∴所求轨迹方程为x2+ y2=5是以(0,0)为圆心,r=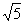 的圆
的圆
(2)t=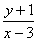 可看作x2+ y2=5上的一点(x,y)与(3,-1)连线的斜率,由图知t的最值,即为圆x2+ y2=5的切线的斜率。设切线方程为y+1=k(x-3),即kx-y-3k-1=0
可看作x2+ y2=5上的一点(x,y)与(3,-1)连线的斜率,由图知t的最值,即为圆x2+ y2=5的切线的斜率。设切线方程为y+1=k(x-3),即kx-y-3k-1=0
∴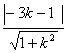 =
=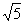 ,即2k2+3k-2=0,
,即2k2+3k-2=0,
∴k=-2或 k=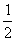
∴tmax=-2,tmin=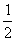

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
