题目内容
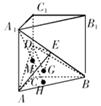
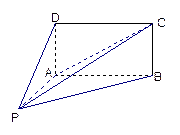
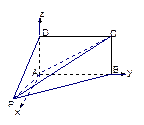
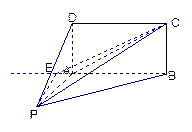
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA="AD=1,AB=2," 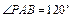 ,
,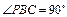 .
.
(1)求证:平面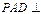 平面
平面 ;
;
(2)求三棱锥D-PAC的体积;
(3)求直线PC与平面ABCD所成角的正弦值.
 ,
, .
.(1)求证:平面
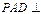 平面
平面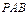 ;
;(2)求三棱锥D-PAC的体积;
(3)求直线PC与平面ABCD所成角的正弦值.

(1)证明:∵ABCD为矩形
∴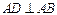 且
且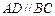 ∵
∵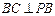 ∴
∴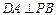 且
且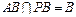
∴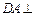 平面
平面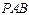 ,又∵
,又∵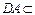 平面PAD ∴平面
平面PAD ∴平面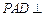 平面
平面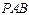
(2) ∵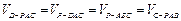 ……… 5分
……… 5分
由(1)知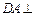 平面
平面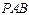 ,且
,且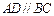 ∴
∴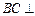 平面
平面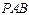 ……… 6分
……… 6分
∴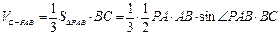
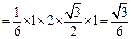 ……… 8分
……… 8分
(3)解法1:以点A为坐标原点,AB所在的直线为y轴建立空间直角坐标系如右图示,则依题意可得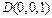 ,
,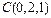 ,
,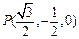
可得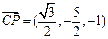 , ……… 10分
, ……… 10分
平面ABCD的单位法向量为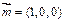 ,设直线PC与平面ABCD所成角为
,设直线PC与平面ABCD所成角为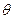 ,
,
则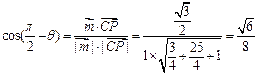
∴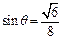 ,即直线PC与平面ABCD所成角的正弦值
,即直线PC与平面ABCD所成角的正弦值
∴
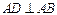 且
且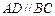 ∵
∵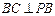 ∴
∴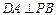 且
且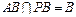
∴
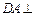 平面
平面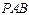 ,又∵
,又∵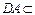 平面PAD ∴平面
平面PAD ∴平面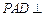 平面
平面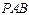

(2) ∵
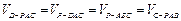 ……… 5分
……… 5分由(1)知
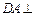 平面
平面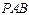 ,且
,且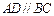 ∴
∴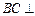 平面
平面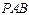 ……… 6分
……… 6分∴
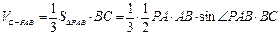
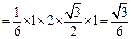 ……… 8分
……… 8分(3)解法1:以点A为坐标原点,AB所在的直线为y轴建立空间直角坐标系如右图示,则依题意可得
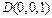 ,
,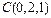 ,
,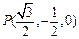
可得
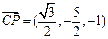 , ……… 10分
, ……… 10分平面ABCD的单位法向量为
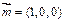 ,设直线PC与平面ABCD所成角为
,设直线PC与平面ABCD所成角为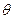 ,
,则
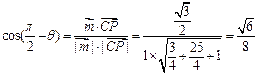
∴
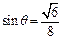 ,即直线PC与平面ABCD所成角的正弦值
,即直线PC与平面ABCD所成角的正弦值
略

练习册系列答案
相关题目
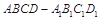 ,中,
,中,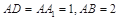 ,点
,点 在棱AB上移动.
在棱AB上移动.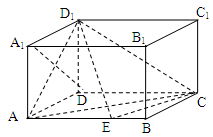
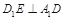 ;
; 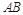 的中点时,求点
的中点时,求点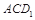 的距离;
的距离; 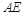 等于何值时,二面角
等于何值时,二面角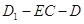 的大小为
的大小为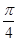 .
.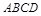 中,
中,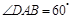 .点
.点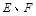 分别在边
分别在边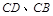 上,点
上,点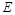 与点
与点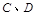 不重合,
不重合,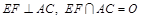 .沿
.沿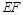 将
将 翻折到
翻折到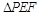 的位置,使平面
的位置,使平面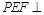 平面
平面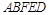 .
.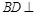 平面
平面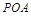 ;
;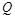 满足
满足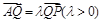 ,试探究:当
,试探究:当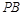 取得最小值时,直线
取得最小值时,直线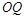 与平面
与平面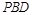 所成角的大小是否一定大于
所成角的大小是否一定大于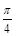 ?并说明理由.
?并说明理由.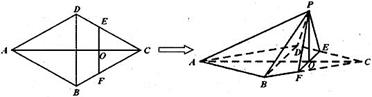
 中,
中,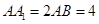 ,点
,点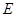 在
在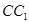 上且
上且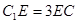 .
.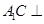 平面
平面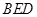 ;
;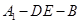 的余弦值大小.
的余弦值大小.
 并确定
并确定 的关系,使
的关系,使 轴垂直.
轴垂直.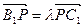 ,当 B1D⊥面PMN时,求
,当 B1D⊥面PMN时,求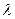 的值.
的值.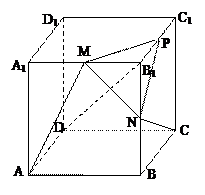
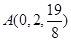 ,
,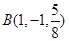 ,
,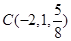 是平面
是平面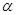 内的三点,设平面
内的三点,设平面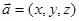 ,则
,则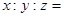 .
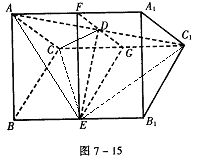
.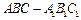 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,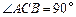 ,侧棱
,侧棱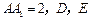 分别是
分别是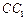 与
与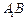 的中点,点
的中点,点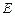 在平面
在平面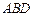 上的射影是
上的射影是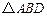 的重心
的重心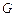 ,求点
,求点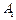 到平面
到平面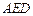 的距离.
的距离.