题目内容
A=C≠0且B=0是方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的 .
【答案】分析:根据x2+y2+Dx+Ey+F=0是圆的标准方程,它表示圆的充要条件是D2+E2-4F>0,结合这个充要条件,比较所给的二元二次方程的表达式,得到前者是后者的必要不充分条件.
解答:解:∵A=C≠0且B=0
∴方程Ax2+Bxy+Cy2+Dx+Ey+F=0变形为Ax2+Cy2+Dx+Ey+F=0,
即x2+y2+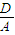 x+
x+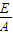 y+
y+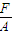 =0
=0
本方程要表示圆,还要满足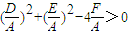 ,
,
∴方程表示圆一定能够推出A=C≠0且B=0,
反过来不成立,
故答案为:必要非充分条件
点评:本题考查二元二次方程表示圆的条件,注意各项的系数之间的关系,本题是一个基础题,若出现则是一个送分题目.
解答:解:∵A=C≠0且B=0
∴方程Ax2+Bxy+Cy2+Dx+Ey+F=0变形为Ax2+Cy2+Dx+Ey+F=0,
即x2+y2+
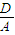 x+
x+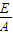 y+
y+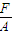 =0
=0本方程要表示圆,还要满足
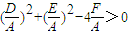 ,
,∴方程表示圆一定能够推出A=C≠0且B=0,
反过来不成立,
故答案为:必要非充分条件
点评:本题考查二元二次方程表示圆的条件,注意各项的系数之间的关系,本题是一个基础题,若出现则是一个送分题目.

练习册系列答案
相关题目