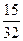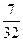题目内容
一项“过关游戏”规则规定：在第n关要抛掷一颗骰子n次，如果这n次抛掷所出现的点数之和大于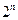
，则算过关。问：（Ⅰ）某人在这项游戏中最多能过几关？（Ⅱ）他连过前三关的概率是多少？（注：骰子是一个在各面上分别有1，2，3，4，5，6点数的均匀正方体。抛掷骰子落地静止后，向上一面的点数为出现点数。）
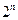，则算过关。问：（Ⅰ）某人在这项游戏中最多能过几关？（Ⅱ）他连过前三关的概率是多少？（注：骰子是一个在各面上分别有1，2，3，4，5，6点数的均匀正方体。抛掷骰子落地静止后，向上一面的点数为出现点数。）
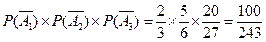
由于骰子是均匀的正方体，所以抛掷后各点数出现的可能性是相等的。
（Ⅰ）因骰子出现的点数最大为6，而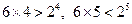
，因此，当
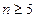时，n次出现的点数之和大于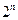已不可能。即这是一个不可能事件，过关的概率为0。所以最多只能连过4关。 .......5分
（Ⅱ）设事件
为“第n关过关失败”，则对立事件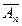
为“第n关过关成功”。
第n关游戏中，基本事件总数为
个。
第1关：事件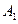
所含基本事件数为2（即出现点数为1和2这两种情况），
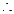过此关的概率为：
。
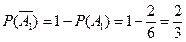第2关：事件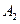
所含基本事件数为方程
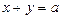当a分别取2，3，4时的正整数解组数之和。即有
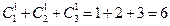（个）。
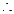过此关的概率为：
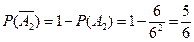。 ........10分
第3关：事件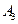
所含基本事件为方程
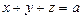当a分别取3，4，5，6，7，8时的正整数解组数之和。即有
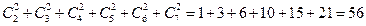（个）。
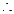过此关的概率为：
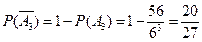。 .........15分
故连过前三关的概率为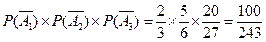：。 .....20分
（说明：第2，3关的基本事件数也可以列举出来）
（Ⅰ）因骰子出现的点数最大为6，而
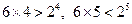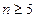，因此，当时，n次出现的点数之和大于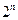已不可能。即这是一个不可能事件，过关的概率为0。所以最多只能连过4关。 .......5分（Ⅱ）设事件
为“第n关过关失败”，则对立事件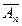为“第n关过关成功”。第n关游戏中，基本事件总数为
个。第1关：事件
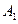所含基本事件数为2（即出现点数为1和2这两种情况），过此关的概率为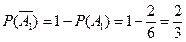：。第2关：事件
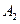所含基本事件数为方程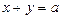当a分别取2，3，4时的正整数解组数之和。即有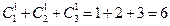（个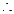）。过此关的概率为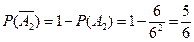：。 ........10分第3关：事件
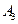所含基本事件为方程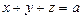当a分别取3，4，5，6，7，8时的正整数解组数之和。即有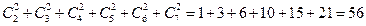（个）。过此关的概率为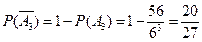：。 .........15分故连过前三关的概率为：
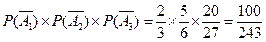。 .....20分（说明：第2，3关的基本事件数也可以列举出来）
练习册系列答案
相关题目
的等差数列，他第一次测试合格的概率不超过
，且他直到第二次测试才合格的概率为
。
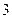
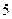
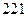
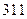
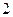
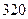
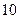
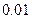元）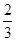
.
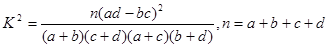
正常工作的概率分别为
，将它们中某两个元件并联后再和第三个元件串联接入电路，在如图的电路中，电路不发生故障的概率是 ( )
