题目内容
以平面直角坐标系的原点为极点,以x轴的正半轴为极轴,建立极坐标系,则曲线
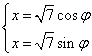 (
(![]() 为参数,
为参数,![]() )上的点到曲线
)上的点到曲线![]() 的最短距离是
的最短距离是
A、0 B、2![]() -
-![]() C、1 D、2
C、1 D、2![]()
B

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
以平面直角坐标系的原点为极点,以x轴的正半轴为极轴,建立极坐标系,则曲线
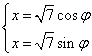 (
(![]() 为参数,
为参数,![]() )上的点到曲线
)上的点到曲线![]() 的最短距离是
的最短距离是
A、0 B、2![]() -
-![]() C、1 D、2
C、1 D、2![]()
B

 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案