题目内容
设a＞0，a≠1，函数f(x)=alg(x2+2x+3)有最大值，则不等式loga(x2-5x+7)＞0的解集为（ ）
分析：函数f(x)=alg(x2+2x+3)有最大值，由于lg（x2-2x+3）≥lg2，可得a的范围，然后解不等式，可求不等式的解集．
解答：解：由于a＞0，a≠1，函数f(x)=alg(x2+2x+3)有最大值，
∵lg（x2-2x+3）≥lg2，所以函数f（x）有最小值，
∴0＜a＜1，则不等式loga（x2-5x+7）＞0的解为 0＜x2-5x+7＜1，
解得2＜x＜3，所以不等式的解集为（2，3），
故选 C．
∵lg（x2-2x+3）≥lg2，所以函数f（x）有最小值，
∴0＜a＜1，则不等式loga（x2-5x+7）＞0的解为 0＜x2-5x+7＜1，
解得2＜x＜3，所以不等式的解集为（2，3），
故选 C．
点评：本题考查指数函数，对数函数的性质，以及一元二次不等式组的解法，属于中档题．
练习册系列答案
相关题目
的定义域为R，若存在与
无关的正常数M，使
对一切实数
；
；
；
．其中是“有界泛函”的个数为 （ ）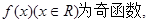
（ ）
D．5
的定义域为R，若存在与
无关的正常数M，使
对一切实数
；
；
；
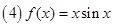．其中是“有界泛函”的个数为 （ ）
)的定义域为R，若存在与
对一切实数
②f(
④
其中是“有界泛函”的个数为（
）
对一切实数x均成立，则称f(x)为“有界泛函”，给出以下函数：①f(x) =x2，②f(x)=2x，③
其中是“有界泛函”的个数为