题目内容
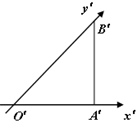 如图,一个水平放置的三角形的斜二侧直观图是等腰直角三角形A′B′O′,若O′A′=2,那么原三角形ABO的最长边的长度为
如图,一个水平放置的三角形的斜二侧直观图是等腰直角三角形A′B′O′,若O′A′=2,那么原三角形ABO的最长边的长度为
- A.

- B.

- C.6
- D.4
C
分析:利用斜二测画法中原图和直观图之间的联系,确定原三角形ABO中,OA=2,OB=4 ,∠AOB=90°,利用勾股定理即可求得结论.
,∠AOB=90°,利用勾股定理即可求得结论.
解答:由图可知,O′A′=2,O′B′=2 ,∠A′O′B′=45°
,∠A′O′B′=45°
∴原三角形ABO中,OA=2,OB=4 ,∠AOB=90°
,∠AOB=90°
∴原三角形ABO的最长边AB=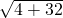 =6
=6
故选C.
点评:本题考查斜二测画法及斜二测画法中原图和直观图之间的联系,考查学生分析解决问题的能力,属于基础题.
分析:利用斜二测画法中原图和直观图之间的联系,确定原三角形ABO中,OA=2,OB=4
 ,∠AOB=90°,利用勾股定理即可求得结论.
,∠AOB=90°,利用勾股定理即可求得结论.解答:由图可知,O′A′=2,O′B′=2
 ,∠A′O′B′=45°
,∠A′O′B′=45°∴原三角形ABO中,OA=2,OB=4
 ,∠AOB=90°
,∠AOB=90°∴原三角形ABO的最长边AB=
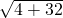 =6
=6故选C.
点评:本题考查斜二测画法及斜二测画法中原图和直观图之间的联系,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
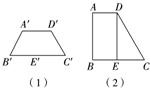 如图,一个水平放置的平面图的斜二测直观图是一个底角为45°、腰和上底长为1的等腰梯形,试画出这个平面图形并求它的面积.
如图,一个水平放置的平面图的斜二测直观图是一个底角为45°、腰和上底长为1的等腰梯形,试画出这个平面图形并求它的面积. 如图,一个水平放置的三角形的斜二侧直观图是等腰直角三角形A′B′O′,若O′A′=2,那么原三角形ABO的最长边的长度为( )
如图,一个水平放置的三角形的斜二侧直观图是等腰直角三角形A′B′O′,若O′A′=2,那么原三角形ABO的最长边的长度为( )
 B.
B. C.
C. D.2
D.2
 B.
B.  C.
C.  D.
D. 
 是一个水平放置的正三棱柱
是一个水平放置的正三棱柱 ,
, 是棱
是棱 的中点.正三棱柱的主视图如图
的中点.正三棱柱的主视图如图 .
.
 的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明) .
.