题目内容
已知函数 ,其中a∈R.
,其中a∈R.(1)若a=2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[2,3]上的最大值.
【答案】分析:(1)把a=2代入解析式,再求出导数,再求出切线的斜率f′(1)和f(1),代入点斜式方程再化为一般式;
(2)由题意求出导数并配方,对a进行分类:a≤0和a>0讨论,再a>0情况下再分类,求出对应的临界点,判断出在[2,3]上的单调性,求出函数的最大值,最后在用分段函数的形式表示出来.
解答:解:(1)当a=2时, ,
,
则f′(x)=2x2-4x,故切线的斜率k=f′(1)=-2,
又∵ ,∴切线方程为
,∴切线方程为  ,
,
即6x+3y-5=0.
(2)由题意得f′(x)=2x2-4x+2-a=2(x-1)2-a,
当a≤0时,f′(x)≥0,∴f(x)在[2,3]上单调递增,
则f(x)max=f(3)=7-3a,
当a>0时,令f′(x)=0,得
①当0<a≤2时,f(x)在[2,3]上单调递增,则f(x)max=f(3)=7-3a
②当2<a<8时,f(x)在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
比较f(2)与f(3)的大小,令f(2)>f(3),
 >
> ,
,
解得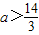 ,
,
③当a≥8时,f(x)在[2,3]上单调递减,
综上,
点评:本题考查了导数的几何意义,以及导数与函数的单调性、最值之间的关系,考查了分类讨论思想和做差法比较大小,属于中档题.
(2)由题意求出导数并配方,对a进行分类:a≤0和a>0讨论,再a>0情况下再分类,求出对应的临界点,判断出在[2,3]上的单调性,求出函数的最大值,最后在用分段函数的形式表示出来.
解答:解:(1)当a=2时,
 ,
,则f′(x)=2x2-4x,故切线的斜率k=f′(1)=-2,
又∵
 ,∴切线方程为
,∴切线方程为  ,
,即6x+3y-5=0.
(2)由题意得f′(x)=2x2-4x+2-a=2(x-1)2-a,
当a≤0时,f′(x)≥0,∴f(x)在[2,3]上单调递增,
则f(x)max=f(3)=7-3a,
当a>0时,令f′(x)=0,得

①当0<a≤2时,f(x)在[2,3]上单调递增,则f(x)max=f(3)=7-3a
②当2<a<8时,f(x)在
 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,比较f(2)与f(3)的大小,令f(2)>f(3),
 >
> ,
,解得
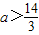 ,
,③当a≥8时,f(x)在[2,3]上单调递减,

综上,

点评:本题考查了导数的几何意义,以及导数与函数的单调性、最值之间的关系,考查了分类讨论思想和做差法比较大小,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.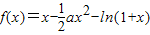 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.