题目内容
i+i2+i3+…+i2005=________.
i
分析:根据虚数单位的性质看出要求的和式中每四项之和等于0,则用2005除以4得到余数是1,则要求的和式等于i2005,求解i2005即可得到结果.本题也可以运用推导等比数列的求和公式的方法,即错位相减法求解.
解答:法一
∵i+i2+i3+i4=i-1-i+1=0,
∴复数z=i+i2+i3+…+i2005
=(i+i2+i3+i4)+(i5+i6+i7+i8)+…+(i2001+i2002+i2003+i2004)+i2005
=i2005
=(i2)1002•i
=(-1)1002•i
=i.
所以i+i2+i3+…+i2005=i.
故答案为i.
法二
设S=i+i2+i3+…+i2005①
等式两边同时乘以i得:
iS=i2+i3+…+i2006②
①-②得:(1-i)S=i-i2006,
所以,S=
=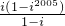
=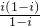
=i.
故答案为i.
点评:本题考查虚数单位的性质及其应用,训练了实数运算中的错位相减法在计算复数题中的运用,此题也可以运用等比数列求和公式求解,是基础题.
分析:根据虚数单位的性质看出要求的和式中每四项之和等于0,则用2005除以4得到余数是1,则要求的和式等于i2005,求解i2005即可得到结果.本题也可以运用推导等比数列的求和公式的方法,即错位相减法求解.
解答:法一
∵i+i2+i3+i4=i-1-i+1=0,
∴复数z=i+i2+i3+…+i2005
=(i+i2+i3+i4)+(i5+i6+i7+i8)+…+(i2001+i2002+i2003+i2004)+i2005
=i2005
=(i2)1002•i
=(-1)1002•i
=i.
所以i+i2+i3+…+i2005=i.
故答案为i.
法二
设S=i+i2+i3+…+i2005①
等式两边同时乘以i得:
iS=i2+i3+…+i2006②
①-②得:(1-i)S=i-i2006,
所以,S=

=
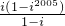
=
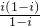
=i.
故答案为i.
点评:本题考查虚数单位的性质及其应用,训练了实数运算中的错位相减法在计算复数题中的运用,此题也可以运用等比数列求和公式求解,是基础题.

练习册系列答案
相关题目