题目内容
(2013•大兴区一模)已知函数f(x)=
在区间[-1,m]上的最大值是1,则m的取值范围是
|
(-1,1]
(-1,1]
.分析:对参数m分类讨论,利用函数的单调性,解出不等式f(m)<1即可.
解答:解:①当m≤0时,f(x)=2-x-1在区间[-1,m]上为减函数
故f(m)=2-m-1<1,
故2-m<2=21,解得m>-1,
则此时-1<m≤0;
②当m>0时,f(x)=2-x-1在区间[-1,0]上为减函数,
f(x)=x
在区间[0,m]上为增函数,故f(m)=m
≤1,
解得0<m≤1.
综上可知,则m的取值范围是(-1,1].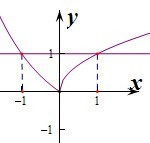
故答案为:(-1,1].
故f(m)=2-m-1<1,
故2-m<2=21,解得m>-1,
则此时-1<m≤0;
②当m>0时,f(x)=2-x-1在区间[-1,0]上为减函数,
f(x)=x
| 1 |
| 2 |
| 1 |
| 2 |
解得0<m≤1.
综上可知,则m的取值范围是(-1,1].

故答案为:(-1,1].
点评:本题为考查函数的单调性,以及分段函数求函数值的问题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 (2013•大兴区一模)执行如图所示的程序框图.若n=5,则输出s的值是( )
(2013•大兴区一模)执行如图所示的程序框图.若n=5,则输出s的值是( )