题目内容
如下图,在△ABC中,BC边的中点M为(-![]() ,
,![]() ),直线AC的方程为x+1=0,直线AB的方程为x+y-1=0,求直线BC的方程.
),直线AC的方程为x+1=0,直线AB的方程为x+y-1=0,求直线BC的方程.

答案:
解析:
提示:
解析:
|
解法一:利用两点式. 设B(a,1-a)、C(-1,b), 则 ∴ ∴BC的方程为 解法二:利用点斜式. 设直线BC的方程为y- 由 ∴由中点坐标公式,得 ∴直线BC的方程为3x+y+7=0. 解法三:利用两点式. 作MD∥AC交AB于D,则点D(- ∵A(-1,2),∴B(-4,5). ∴由点M、B的坐标可得,直线BC的方程为3x+y+7=0. |
提示:
|
确定直线的方程需要两个条件,本题已经给出直线BC经过M点,所以只要求得点B(或C)的坐标或直线BC的斜率就可以了. |

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
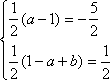
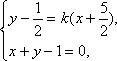 得B点横坐标xB=
得B点横坐标xB=
 =
= ,
, =
= ,AP的中点为Q,BQ的中点为R,CR的中点为P,若
,AP的中点为Q,BQ的中点为R,CR的中点为P,若 =m
=m ( )
( ) 




 =
= ,
, =
= ,AP的中点为Q,BQ的中点为R,CR的中点为P,若
,AP的中点为Q,BQ的中点为R,CR的中点为P,若 =m
=m ( )
( ) 
 B.
B. C.
C. D.
D.