题目内容

给出下列三个命题：

①若a≥b>-1，则.

②若正整数m和n满足m≤n，则.

③设P（x1，y1）为圆O1：x2+y2=9上任一点，圆O2以Q（a，b）为圆心且半径为1.

当(a-x1)2+(b-y1)2=1时，圆O1与圆O2相切.

其中假命题的个数为

（A）0     （B）1      （C）2     （D）3

B

解析：∵a≥b＞－1，∴a+1≥b+1＞0，

≥a（1+b）≥b（1+a） a≥b.

∵a≥b成立，∴≥.

故命题①是真命题.

∵0＜m≤n，∴n－m≥0.

当n－m=0时， =0，＞0，

∴≤.

当n－m＞0时， ≤=.

∴命题②是真命题.

∵（a－x1）2+（b－y1）2=1，

∴圆O2的圆心与圆O1的圆心距离是1.

如下图所示知，圆O2与圆O1可能相割，

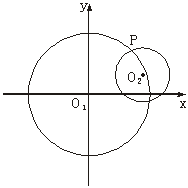
∴命题③是假命题.故选B.

 


练习册系列答案
相关题目
关于函数f(x)=sinx(cosx-sinx)+
1
2
，给出下列三个命题：
（1）函数f（x）在区间[
π
2
，
5π
8
]上是减函数；
（2）直线x=
π
8
是函数f（x）的图象的一条对称轴；
（3）函数f（x）的图象可以由函数y=
2
2
sin2x的图象向左平移
π
4
而得到．
其中正确的命题序号是
 
．（将你认为正确的命题序号都填上）
给出下列三个命题：
①函数y=
1
2
ln
1-cosx
1+cosx
与y=lntan
x
2
是同一函数；
②若函数y=f（x）与y=g（x）的图象关于直线y=x对称，则函数y=f（2x）与y=
1
2
g(x)的图象也关于直线y=x对称；
③若奇函数f（x）对定义域内任意x都有f（x）=f（2-x），则f（x）为周期函数．
其中真命题是（　　）
A、①②B、①③C、②③D、②
14、已知直线m，n与平面α，β，给出下列三个命题：①若m∥α，n∥α，则m∥n；②若m∥α，n⊥α，则n⊥m；③若m⊥α，m∥β，则α⊥β其中正确命题的序号是
②③
．
给出下列三个命题：
①函数y=ax（a＞0且a≠1）与函数y=logax（a＞0且a≠1）的定义域相同；
②函数y=x3与y=3x的值域相同；
③函数y=
1
2
+
1
2x-1
与y=lg(x+
x2+1
)都是奇函数．
其中正确命题的序号是
①③
①③
（把你认为正确的命题序号都填上）．
（2000•上海）设有不同的直线a、b和不同的平面α、β、γ，给出下列三个命题：
（1）若a∥α，b∥α，则a∥b．
（2）若a∥α，a∥β，则α∥β．
（3）若a∥γ，β∥γ，则a∥β．
其中正确的个数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网