题目内容
若函数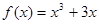
对任意的
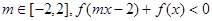恒成立，则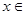
___________.
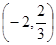
解析试题分析：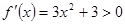
，所以函数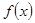
在R上单调递增，又
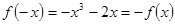，所以函数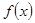为奇函数，于是
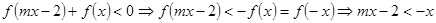，因为对任意的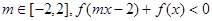恒成立，所以
.
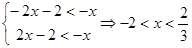考点：导数判断函数的单调性、解不等式.
练习册系列答案
智能训练练测考系列答案
相关题目
智能训练练测考系列答案题目内容
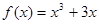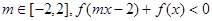若函数对任意的恒成立，则___________.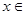
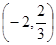
解析试题分析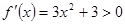：，所以函数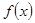在R上单调递增，又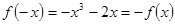，所以函数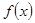为奇函数，于是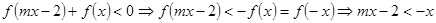，因为对任意的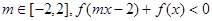恒成立，所以.
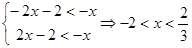考点：导数判断函数的单调性、解不等式.
智能训练练测考系列答案
的单调增区间是 ．
和
在它们的交点处的两条切线与
轴所围成的三角形的面积是 ．
，则函数
的图象在点
处的切线方程是 .
在
处的切线方程为 ． 
，
所围成的封闭图形的面积为 .
=____________________.
在
上可导，
，则
.
，且
，
，
，下列命题：
，则
，
，使得
，
，则
，都有