题目内容
已知tanα=![]() ,求下列各式的值.
,求下列各式的值.
(1)![]() ;(2)2sin2α-
;(2)2sin2α-![]() sinαcosα+5cos2α;(3)
sinαcosα+5cos2α;(3)![]() .
.
分析:由于已知条件为切,所求式为弦,故应想办法将切化弦,或将弦化切(这是一种分析综合的思想);若切化弦,应把条件tanα=![]() =
=![]() 代入所求式,消去其中一种函数名,再进一步求值;若弦化切,应把所求式化成用tanα表示的式子,一般说关于sinα和cosα的齐次式都可化为关于tanα的函数式.
代入所求式,消去其中一种函数名,再进一步求值;若弦化切,应把所求式化成用tanα表示的式子,一般说关于sinα和cosα的齐次式都可化为关于tanα的函数式.
解:(1)由tanα=![]()
得cosα=-3sinα, 代入所求式得
![]() .
.
(2)原式= ·cos2α
·cos2α
=(2tan2α-![]() tanα+5)·
tanα+5)·![]() .
.
将tanα=![]() 代入得:
代入得:
原式=(2×![]() )·
)·![]() =
=![]() .
.
(3)原式= .
.
点评:一般地,形如![]() ,可利用分子、分母同除以cosα,cos2α转化为关于tanα的表达式.
,可利用分子、分母同除以cosα,cos2α转化为关于tanα的表达式.

练习册系列答案
相关题目
 )(x∈R),且
)(x∈R),且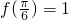 .
.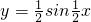 的图象;
的图象;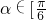 ,
, ,
,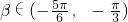 ,
,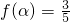 ,f(β)=-
,f(β)=- ,
,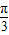 )(x∈R),且
)(x∈R),且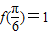 .
.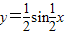 的图象;
的图象;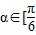 ,
,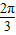 ,
,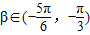 ,
,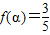 ,f(β)=-
,f(β)=- ,
,