题目内容
已知抛物线的顶点在坐标原点 ,焦点
,焦点 在
在 轴上,抛物线上的点
轴上,抛物线上的点 到
到 的距离为2,且
的距离为2,且 的横坐标为1.直线
的横坐标为1.直线 与抛物线交于
与抛物线交于 ,
, 两点.
两点.
(1)求抛物线的方程;
(2)当直线 ,
, 的倾斜角之和为
的倾斜角之和为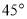 时,证明直线
时,证明直线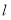 过定点.
过定点.
(1)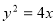 ;(2)直线
;(2)直线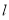 恒过定点
恒过定点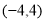 ,证明详见解析.
,证明详见解析.
【解析】
试题分析:(1)设抛物线方程为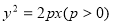 ,由抛物线的定义及
,由抛物线的定义及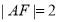 即可求得
即可求得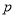 的值;(2)先设点
的值;(2)先设点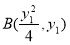 ,
,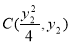 ,然后将直线方程与抛物线方程联立消去
,然后将直线方程与抛物线方程联立消去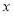 得
得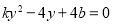 ,根据二次方程根与系数的关系表示出
,根据二次方程根与系数的关系表示出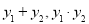 ,设直线
,设直线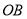 ,
,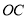 的倾斜角分别为
的倾斜角分别为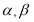 ,斜率分别为
,斜率分别为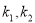 ,则
,则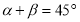 ,进而根据正切的两角和公式可知
,进而根据正切的两角和公式可知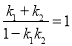 ,其中
,其中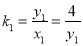 ,
,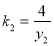 ,代入
,代入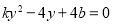 求得
求得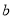 和
和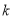 的关系式,此时使
的关系式,此时使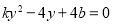 有解的
有解的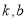 有无数组,把直线方程整理得
有无数组,把直线方程整理得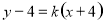 ,推断出直线
,推断出直线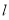 过定点
过定点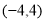 .
.
试题解析:(1)设抛物线方程为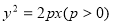
由抛物线的定义知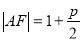 ,又
,又 2分
2分
所以 ,所以抛物线的方程为
,所以抛物线的方程为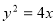 4分
4分
(2)设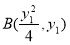 ,
,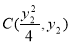
联立 ,整理得
,整理得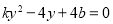 (依题意
(依题意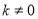 )
)
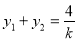 ,
,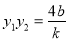 6分
6分
设直线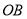 ,
,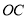 的倾斜角分别为
的倾斜角分别为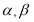 ,斜率分别为
,斜率分别为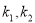 ,则
,则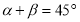
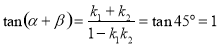 8分
8分
其中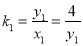 ,
,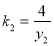 ,代入上式整理得
,代入上式整理得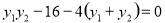
所以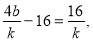 即
即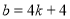 10分
10分
直线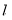 的方程为
的方程为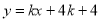 ,整理得
,整理得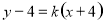
所以直线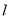 过定点
过定点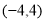 12分.
12分.
考点:1.抛物线的定义与方程;2.直线与抛物线的综合问题;3.二次方程根与系数的关系.

练习册系列答案
相关题目