题目内容
设n∈N*且n≥2,证明不等式
证明:(1)先证左端不等号成立.
①n=2时,1+![]() 成立.
成立.
②设n=k(k≥2)时,1+![]() >
>![]() 成立.
成立.
当n=k+1时,有1+![]()
=![]()
=![]()
>![]() ,
,
即n=k+1时,1+![]() 成立.
成立.
由①②知,对于任何n∈N*(n≥2)不等式左端成立.
(2)再证右端不等式,
①当n=2时,1+![]() 成立.
成立.
②假设n=k时,![]() <
<![]() 成立,
成立,
当n=k+1时,![]() ,
,
下面证明![]() ,
,
∵![]() (基本不等式放缩)=
(基本不等式放缩)=![]() =0,
=0,
∴![]() ,
,
即当n=k+1时,![]() 成立.
成立.
由①②知对任意n∈N*(n≥2)不等式右端成立.
综上两部分证明知原不等式成立.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
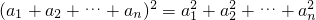 +2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].
+2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an]. …
… 对一切n∈N*且n≥2恒成立,求实数k的取值范围.
对一切n∈N*且n≥2恒成立,求实数k的取值范围.