题目内容
设数列{an}是以a为首项,t为公比的等比数列,令bn=1+a1+a2+…+an,cn=2+b1+b2+…+bn,n∈N(1)试用a,t表示bn和cn
(2)若a>0,t>0且t≠1,试比较cn与cn+1(n∈N)的大小
(3)是否存在实数对(a,t),其中t≠1,使得{cn}成等比数列,若存在,求出实数对(a,t)和{cn};若不存在说明理由.
【答案】分析:(1)注意到bn=1+a1+a2+…+an除 首项,其余是数列{an} 各项,按照等比数列求和公式可表示出bn,再去求cn.注意对公比t是否为1进行讨论.
(2) ,由此再判判断.
,由此再判判断.
(3) ,若成等比数列,根据通项公式特点须
,若成等比数列,根据通项公式特点须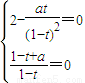 研究方程组解得情况,做出判断.
研究方程组解得情况,做出判断.
解答:解:(1)当t=1时,an=a1=a,bn=1+na,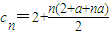
当t≠1时,an=atn-1,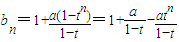
∴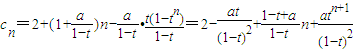
(2)
当t>1时,1-t<0,1-tn+1<0,而已知a>0,∴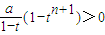 ∴cn+1-cn>0
∴cn+1-cn>0
同理当0<t<1时,1-t>0,1-tn+1>0,而已知a>0,∴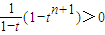 ∴cn+1-cn>0
∴cn+1-cn>0
综上所述cn+1>cn
(3)若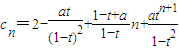 成等比数列,则令
成等比数列,则令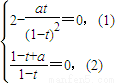
由(2),得a=t-1代入(1),得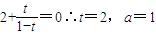
此时cn=2n+1=4×2n-1
所以存在实数对(a,t)为(1,2),使得{cn}成为以4为首项,2为公比的等比数列.
点评:本题考查等差、等比数列求和,代数式大小比较,方程组求解问题,考查计算、转化,分类讨论等思想方法和能力.
(2)
 ,由此再判判断.
,由此再判判断.(3)
 ,若成等比数列,根据通项公式特点须
,若成等比数列,根据通项公式特点须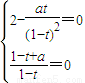 研究方程组解得情况,做出判断.
研究方程组解得情况,做出判断.解答:解:(1)当t=1时,an=a1=a,bn=1+na,
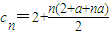
当t≠1时,an=atn-1,
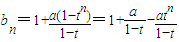
∴
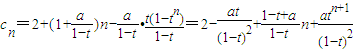
(2)

当t>1时,1-t<0,1-tn+1<0,而已知a>0,∴
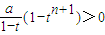 ∴cn+1-cn>0
∴cn+1-cn>0同理当0<t<1时,1-t>0,1-tn+1>0,而已知a>0,∴
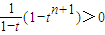 ∴cn+1-cn>0
∴cn+1-cn>0综上所述cn+1>cn
(3)若
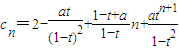 成等比数列,则令
成等比数列,则令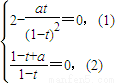
由(2),得a=t-1代入(1),得
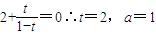
此时cn=2n+1=4×2n-1
所以存在实数对(a,t)为(1,2),使得{cn}成为以4为首项,2为公比的等比数列.
点评:本题考查等差、等比数列求和,代数式大小比较,方程组求解问题,考查计算、转化,分类讨论等思想方法和能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设数列{an}是以2为首项,1为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,则ab1+ab2+…+ab10=( )
| A、1033 | B、1034 | C、2057 | D、2058 |
设数列{an}是以2为首项,1为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,则b a1+b a2+…+b a6等于( )
| A、78 | B、84 | C、124 | D、126 |