题目内容
函数f（x）=x3-3x2-9x+3，若函数g（x）=f（x）-m在x∈[-2，5]上有3个零点，则m的取值范围为
- A.（-24，8）
- B.（-24，1]
- C.[1，8]
- D.[1，8）
D
分析：函数g（x）=f（x）-m在x∈[-2，5]上有3个零点，可转化为函数f（x）=x3-3x2-9x+3，与y=m两个函数的图象有三个交点，故求出函数的单调性与极值，对研究出函数的图象的特征，由图象求出m的取值范围即可
解答：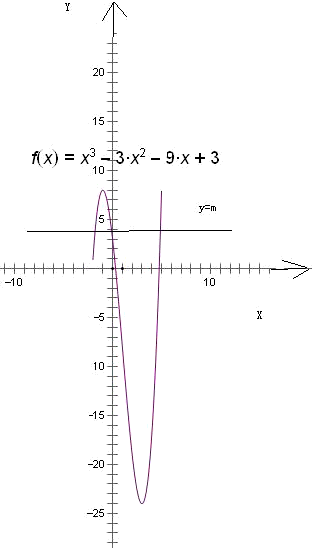
解：函数g（x）=f（x）-m在x∈[-2，5]上有3个零点，即函数f（x）=x3-3x2-9x+3，与y=m两个函数的图象有三个交点，下研究函数f（x）=x3-3x2-9x+3的性质
由题意f'（x）=3x2-6x-9
令f'（x）=3x2-6x-9＞0解得x＞3或x＜-1
又x∈[-2，5]
故f（x）=x3-3x2-9x+3在（-2，-1）与（3，5）上是增函数，在（-1，3）上是减函数，
x=-2，-1，3，5时，函数值对应为1，8，-24，8
其图象如图，可得1≤m＜8
故选D
点评：本题考查根的存在性及根的个数的判断，正确解答本题，关键是将函数有零点的问题转化为两个函数有交点的问题，此转化的好处是转化后的两个函数的中有一个函数是确定的，实现了由不定到定的转化变，方便了研究问题，即求参数的范围．熟练利用导数研究函数的单调性也是解本题的关键，
分析：函数g（x）=f（x）-m在x∈[-2，5]上有3个零点，可转化为函数f（x）=x3-3x2-9x+3，与y=m两个函数的图象有三个交点，故求出函数的单调性与极值，对研究出函数的图象的特征，由图象求出m的取值范围即可
解答：
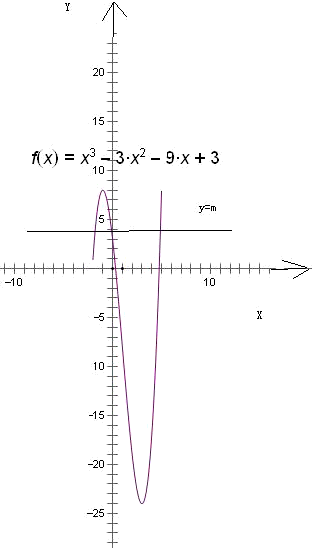解：函数g（x）=f（x）-m在x∈[-2，5]上有3个零点，即函数f（x）=x3-3x2-9x+3，与y=m两个函数的图象有三个交点，下研究函数f（x）=x3-3x2-9x+3的性质由题意f'（x）=3x2-6x-9
令f'（x）=3x2-6x-9＞0解得x＞3或x＜-1
又x∈[-2，5]
故f（x）=x3-3x2-9x+3在（-2，-1）与（3，5）上是增函数，在（-1，3）上是减函数，
x=-2，-1，3，5时，函数值对应为1，8，-24，8
其图象如图，可得1≤m＜8
故选D
点评：本题考查根的存在性及根的个数的判断，正确解答本题，关键是将函数有零点的问题转化为两个函数有交点的问题，此转化的好处是转化后的两个函数的中有一个函数是确定的，实现了由不定到定的转化变，方便了研究问题，即求参数的范围．熟练利用导数研究函数的单调性也是解本题的关键，
练习册系列答案
名校课堂系列答案
相关题目