题目内容

设A={x|x+2≥0}，B={x∈N^*|2x-3≤0}，则A∩B=

A.
$数学公式$
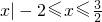
B.
{1}
C.
{-2，-1，0，1}
D.
$数学公式$

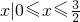
B
分析：集合A与集合B的公共元素构成集合A∩B，由此利用A={x|x+2≥0}={x|x≥-2}，B={x∈N^*|2x-3≤0}={x∈N^*|x≤ $\text{[math]}$ }={1}，能求出A∩B．
解答：∵A={x|x+2≥0}={x|x≥-2}，
B={x∈N^*|2x-3≤0}={x∈N^*|x≤ $\text{[math]}$ }={1}，
∴A∩B={1}．
故选B．
点评：本题考查集合的交集及其运算，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．

练习册系列答案

智能达标AB卷系列答案

智慧金卷26套系列答案

单元加期末冲刺100分系列答案

高效智能课时作业系列答案

高效课堂互动英语系列答案

初中全程导学导练系列答案

期末总复习系列答案

B卷周计划系列答案

天利38套初中名校期末联考测试卷系列答案

捷径训练检测卷系列答案

相关题目

15、（1）设A={x|x=2k-1，k∈Z}，B={x|x=2k，k∈Z}，求C_ZA及C_Z（A∪B）
（2）已知A={x|a-4≤x＜a+3}，B={x|x＜2或x＞5}，且A∩B=A，求a的取值范围．

3、设A={x|x=2^α•3^β，α，β∈Z且α≥0，β≥0}，B={x|1≤x≤5}，则实数A∩B=

{1，2，3，4}

，5]，其中m是不等于零的常数，
（1）（理）写出h（4x）的定义域；
（文）m=1时，直接写出h（x）的值域；
（2）（文、理）求h（x）的单调递增区间；
（3）已知函数f（x）（x∈[a，b]），定义：f₁（x）=minf（t）|a≤t≤x（x∈[a，b]），f₂（x）=maxf（t）|a≤t≤x（x∈[a，b]）．其中，minf（x）|x∈D表示函数f（x）在D上的最小值，maxf（x）|x∈D表示函数f（x）在D上的最大值．例如：f（x）=cosx，x∈[0，π]，则f₁（x）=cosx，x∈[0，π]，f₂（x）=1，x∈[0，π]．
（理）当m=1时，设M(x)=

，不等式t≤M₁（x）-M₂（x）≤n恒成立，求t，n的取值范围；
（文）当m=1时，|h₁（x）-h₂（x）|≤n恒成立，求n的取值范围．

设A={x|x²-2x+a=0}，4∈A，
（1）求a的值，并写出集合A的所有子集；
（2）已知B={x|mx+2=0}，若A∪B=A，求m的值．

设A={x|x+2≥0}，B={x∈N^*|2x-3≤0}，则A∩B=（　　）

A．{x|-2≤x≤

C．{-2，-1，0，1}

D．{x|0≤x≤