题目内容
抛物线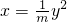 的准线与双曲线
的准线与双曲线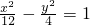 的右准线重合,则m的值是
的右准线重合,则m的值是
- A.-8
- B.-12
- C.4
- D.16
B
分析:先由双曲线方程得出右准线方程,进而求得p,则双曲线准线方程可得,进而求得抛物线方程中的P,则抛物线的焦点坐标可得.
解答:双曲线方程得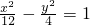 ,
,
∴a=2 ,b=2,c=
,b=2,c=
∴双曲线的右准线方程为x= =3,
=3,
∴抛物线的准线方程为x=3,
∴p=3,
即:- ,m=-12
,m=-12
故选B.
点评:本题主要考查了抛物线的简单性质,圆锥曲线的共同特征.解答的关键是学生对基础知识的综合把握能力.
分析:先由双曲线方程得出右准线方程,进而求得p,则双曲线准线方程可得,进而求得抛物线方程中的P,则抛物线的焦点坐标可得.
解答:双曲线方程得
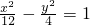 ,
,∴a=2
 ,b=2,c=
,b=2,c=
∴双曲线的右准线方程为x=
 =3,
=3,∴抛物线的准线方程为x=3,
∴p=3,
即:-
 ,m=-12
,m=-12故选B.
点评:本题主要考查了抛物线的简单性质,圆锥曲线的共同特征.解答的关键是学生对基础知识的综合把握能力.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
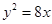 的准线
的准线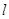 与双曲线
与双曲线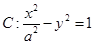 相切,则双曲线
相切,则双曲线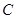 的离心率
的离心率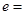 .
. 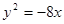 的准线与双曲线
的准线与双曲线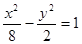 的两条渐近线所围成的三角形的面积为
的两条渐近线所围成的三角形的面积为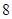 B.
B.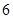 C.
C.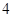 D. 2
D. 2