题目内容
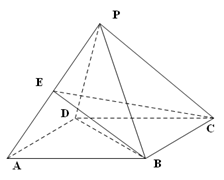
在四棱锥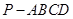 中,侧面
中,侧面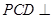 底面
底面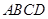 ,
,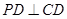 ,
,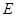 为
为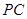 中点,底面
中点,底面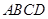 是直角梯形,
是直角梯形,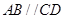 ,
,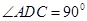 ,
,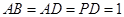 ,
,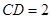 .
.
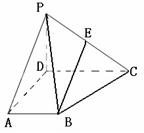
(1)求证: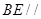 面
面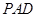 ;
;
(2)求证:面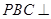 面
面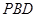 ;
;
(3)设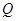 为棱
为棱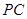 上一点,
上一点,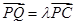 ,试确定
,试确定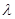 的值使得二面角
的值使得二面角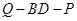 为
为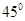 .
.
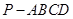 中,侧面
中,侧面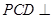 底面
底面 ,
, ,
, 为
为 中点,底面
中点,底面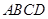 是直角梯形,
是直角梯形,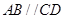 ,
,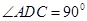 ,
,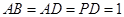 ,
,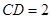 .
.
(1)求证:
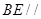 面
面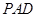 ;
;(2)求证:面
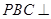 面
面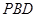 ;
;(3)设
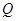 为棱
为棱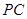 上一点,
上一点,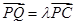 ,试确定
,试确定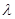 的值使得二面角
的值使得二面角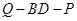 为
为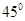 .
.(1)证明过程详见解析;(2)证明过程详见解析;(3)能确定,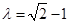 .
.
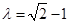 .
.试题分析:(1)先证明
 为平行四边形,所以
为平行四边形,所以 ,即证明
,即证明 ;(2)先证明
;(2)先证明 面
面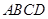 ,所以
,所以 ,再证明
,再证明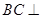 面
面 ,从而得到面
,从而得到面 面
面 ;(3)先建立空间直角坐标系,所以
;(3)先建立空间直角坐标系,所以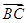 即为面
即为面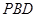 法向量
法向量 ,令面
,令面 法向量为
法向量为 ,利用夹角的余弦求出
,利用夹角的余弦求出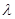 ,又
,又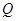 在棱
在棱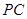 上,所以对
上,所以对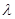 的值进行取舍.
的值进行取舍.试题解析:(1)证明:记
 中点为
中点为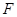 . 连结
. 连结 、
、 ,
,则 AB

 FE
FE 
 所以AB
所以AB  FE 1分
FE 1分所以
 为平行四边形.
为平行四边形. 2分
2分又
 ,
,
 4分
4分(2)连结
 在直角梯形
在直角梯形 中.
中. ,
, ,
, ,所以
,所以 ,
, 5分
5分
 面
面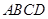

 , 6分
, 6分又
 ,
,  ∴
∴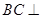 面
面 , 7分
, 7分而
 面
面
 面
面 面
面 8分
8分
(3)以
 为原点,
为原点,  所在直线分别为
所在直线分别为 轴,
轴, 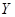 轴,
轴,  轴建立空间直角坐标系.
轴建立空间直角坐标系. ,
, ,
, ,
, ,
,令
 ,∵
,∵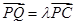 ,∴
,∴ 又
又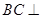 面
面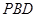
∴
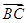 即为面
即为面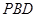 法向量
法向量
又令面
 法向量为
法向量为 ,则
,则

令
 ,∴
,∴
又二面角
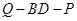 为
为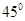
 ,即
,即
解得

又
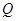 在棱
在棱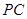 上 ∴
上 ∴ ∴
∴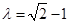 为所求.
为所求.

练习册系列答案
相关题目
 中,点
中,点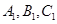 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且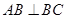 ,
,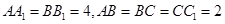 ,E为
,E为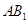 中点,
中点,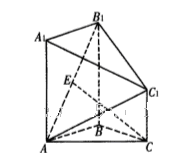
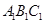 ,
,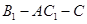 的大小.
的大小. 中,四边形
中,四边形 是菱形,
是菱形,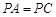 ,E为PB的中点.
,E为PB的中点.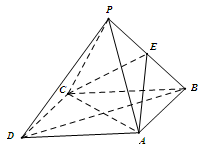
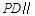 平面
平面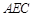 ;
;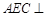 平面
平面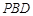 .
. 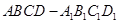 中,
中,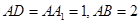 ,点E为AB的中点.
,点E为AB的中点.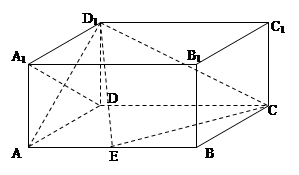
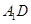 与平面
与平面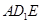 所成的角;
所成的角; 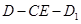 的平面角的正切值.
的平面角的正切值. 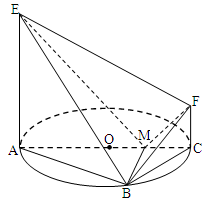
 的底面
的底面 是边长为2的菱形,
是边长为2的菱形, .已知
.已知 .
.
 为
为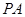 的中点,求三菱锥
的中点,求三菱锥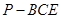 的体积.
的体积.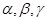 ,若
,若 ,则
,则 ∥
∥
 ,若
,若 ,直线
,直线 与
与 与
与 与棱长为
与棱长为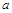 正四面体各面都相切,则该球的表面积为
正四面体各面都相切,则该球的表面积为 ;
; 中,
中, 则
则 .
. 是三条不同的直线,
是三条不同的直线, 是三个不同的平面,则下列命题不正确的是( )
是三个不同的平面,则下列命题不正确的是( ) ∥
∥ ,
, ,则
,则 ∥
∥ ,
, ,则
,则