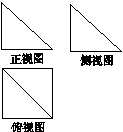
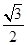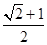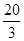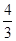题目内容
一个空间几何体的三视图如图所示,则该几何体的表面积为( )
| A.48 | B. | C. | D.80 |
C
解析试题分析:如图所示的三视图是以左视图所示等腰梯形为底的直四棱柱,其底面上底长为2,下底长为4,高为4,故底面积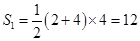 ,腰长为:
,腰长为: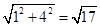 ,则底面周长为:
,则底面周长为: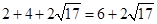 ,则其侧面积
,则其侧面积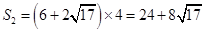 ,则该几何体的表面积为
,则该几何体的表面积为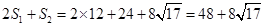 ,故选C.
,故选C.
考点:三视图,几何体的表面积.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
一个简单几何体的主视图、俯视图如图所示,则其左视图不可能为( )
| A.正方形 | B.圆 |
| C.等腰三角形 | D.直角梯形 |
一几何体的三视图如图所示,则该几何体的体积为( )、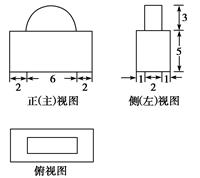
| A.200+9π | B.200+18π |
| C.140+9π | D.140+18π |
一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )
| A.V1<V2<V4<V3 | B.V1<V3<V2<V4 |
| C.V2<V1<V3<V4 | D.V2<V3<V1<V4 |
已知Rt△ABC,其三边分别为a,b,c(a>b>c).分别以三角形的边a,b,c所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,其表面积和体积分别为S1,S2,S3和V1,V2,V3.则它们的大小关系为( )
| A.S1>S2>S3,V1>V2>V3 |
| B.S1<S2<S3,V1<V2<V3 |
| C.S1>S2>S3,V1=V2=V3 |
| D.S1<S2<S3,V1=V2=V3 |
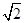 的矩形,则该正方体的正视图的面积等于( )
的矩形,则该正方体的正视图的面积等于( )