题目内容
已知椭圆 的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为
的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.(1)求椭圆的方程;
(2)过点A作直线交椭圆于另一点M,求|AM|长度的最大值;
(3)已知定点E(-1,0),直线y=kx+t与椭圆交于C、D相异两点.证明:对任意的t>0,都存在实数k,使得以线段CD为直径的圆过E点.
【答案】分析:(1)利用c2是a2与b2的等差中项,可得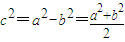 ,设出直线方程,利用直线与原点的距离为
,设出直线方程,利用直线与原点的距离为 ,建立等式,求出几何量,即可求椭圆的方程;
,建立等式,求出几何量,即可求椭圆的方程;
(2)设M的坐标,表示出|AM|2,即可求|AM|长度的最大值;
(3)直线方程代入椭圆方程,利用韦达定理及以CD为直径的圆过E点,结合向量知识,即可得到结论.
解答:(1)解:在椭圆中,由已知得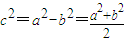 (1分)
(1分)
过点A(0,-b)和B(a,0)的直线方程为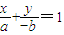 ,即bx-ay-ab=0,
,即bx-ay-ab=0,
该直线与原点的距离为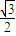 ,由点到直线的距离公式得:
,由点到直线的距离公式得: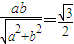 (3分)
(3分)
解得:a2=3,b2=1,所以椭圆方程为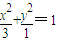 (4分)
(4分)
(2)解:设M(x,y),则x2=3(1-y2),|AM|2=x2+(y+1)2=-2y2+2y+4,其中-1≤y≤1(16分)
当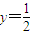 时,|AM|2取得最大值
时,|AM|2取得最大值 ,所以|AM|长度的最大值为
,所以|AM|长度的最大值为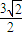 (9分)
(9分)
(3)证明:将y=kx+t代入椭圆方程,得(1+3k2)x2+6ktx+3t2-3=0,
由直线与椭圆有两个交点,所以△=(6kt)2-12(1+3k2)(t2-1)>0,解得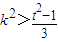 (11分)
(11分)
设C(x1,y1)、D(x2,y2),则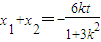 ,
,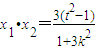 ,
,
因为以CD为直径的圆过E点,所以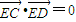 ,即(x1+1)(x2+1)+y1y2=0,(13分)
,即(x1+1)(x2+1)+y1y2=0,(13分)
而y1y2=(kx1+t)(kx2+t)=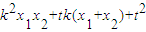 ,
,
所以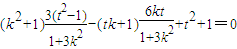 ,解得
,解得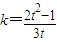 (14分)
(14分)
如果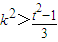 对任意的t>0都成立,则存在k,使得以线段CD为直径的圆过E点.
对任意的t>0都成立,则存在k,使得以线段CD为直径的圆过E点.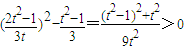 ,即
,即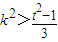 .
.
所以,对任意的t>0,都存在k,使得以线段CD为直径的圆过E点.(16分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.
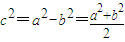 ,设出直线方程,利用直线与原点的距离为
,设出直线方程,利用直线与原点的距离为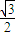 ,建立等式,求出几何量,即可求椭圆的方程;
,建立等式,求出几何量,即可求椭圆的方程;(2)设M的坐标,表示出|AM|2,即可求|AM|长度的最大值;
(3)直线方程代入椭圆方程,利用韦达定理及以CD为直径的圆过E点,结合向量知识,即可得到结论.
解答:(1)解:在椭圆中,由已知得
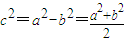 (1分)
(1分)过点A(0,-b)和B(a,0)的直线方程为
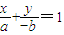 ,即bx-ay-ab=0,
,即bx-ay-ab=0,该直线与原点的距离为
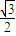 ,由点到直线的距离公式得:
,由点到直线的距离公式得: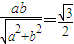 (3分)
(3分)解得:a2=3,b2=1,所以椭圆方程为
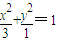 (4分)
(4分)(2)解:设M(x,y),则x2=3(1-y2),|AM|2=x2+(y+1)2=-2y2+2y+4,其中-1≤y≤1(16分)
当
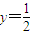 时,|AM|2取得最大值
时,|AM|2取得最大值 ,所以|AM|长度的最大值为
,所以|AM|长度的最大值为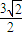 (9分)
(9分)(3)证明:将y=kx+t代入椭圆方程,得(1+3k2)x2+6ktx+3t2-3=0,
由直线与椭圆有两个交点,所以△=(6kt)2-12(1+3k2)(t2-1)>0,解得
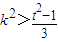 (11分)
(11分)设C(x1,y1)、D(x2,y2),则
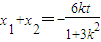 ,
,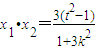 ,
,因为以CD为直径的圆过E点,所以
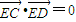 ,即(x1+1)(x2+1)+y1y2=0,(13分)
,即(x1+1)(x2+1)+y1y2=0,(13分)而y1y2=(kx1+t)(kx2+t)=
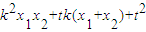 ,
,所以
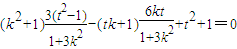 ,解得
,解得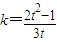 (14分)
(14分)如果
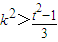 对任意的t>0都成立,则存在k,使得以线段CD为直径的圆过E点.
对任意的t>0都成立,则存在k,使得以线段CD为直径的圆过E点.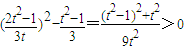 ,即
,即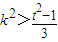 .
.所以,对任意的t>0,都存在k,使得以线段CD为直径的圆过E点.(16分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ),(1,0),椭圆的长半轴长为2,则椭圆方程为( )
),(1,0),椭圆的长半轴长为2,则椭圆方程为( ) B.
B.
 D.
D.
 的两个焦点为F1、F2,椭圆上一点
的两个焦点为F1、F2,椭圆上一点 满足
满足
 与椭圆恒有两上不同的交点A、B,且
与椭圆恒有两上不同的交点A、B,且 (O是坐标原点),求k的范围。
(O是坐标原点),求k的范围。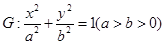 的两个焦点为
的两个焦点为 、
、 ,点
,点 在椭圆G上,且
在椭圆G上,且 ,且
,且 ,斜率为1的直线
,斜率为1的直线 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2). 的面积.
的面积. ,
, ,
, 是椭圆上一点,
是椭圆上一点, ,
, ,则该椭圆的方程是( )
,则该椭圆的方程是( )  B、
B、 C、
C、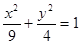 D、
D、