题目内容
下列四种说法:①命题“?x∈R,使得x2+1>3x”的否定是“?x∈R,都有x2+1≤3x”;
②设p、q是简单命题,若“p∨q”为假命题,则“¬p∧¬q”为真命题;
③把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移
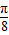 个单位即可得到函数
个单位即可得到函数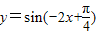 (x∈R)的图象.
(x∈R)的图象.其中所有正确说法的序号是 .
【答案】分析:①根据命题否定的规则进行判断;
②已知p、q是简单命题,若“p∨q”为假命题,可得p与q都为假命题,然后再进行判断;
③把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移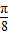 个单位,即把x变为x-
个单位,即把x变为x-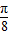 ,代入化简进行判断;
,代入化简进行判断;
解答:解:①∵命题“?x∈R,使得x2+1>3x”,知“存在”的否定词为“任意”,
∴命题的否定为“?x∈R,都有x2+1≤3x”;故①正确;
②∵“p∪q”为假命题,∴p和q都为假命题,∴“¬p与¬q都为真命题,∴¬p∩¬q为真,故②正确;
③∵把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移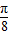 个单位,
个单位,
∴y=sin[-2(x-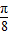 )]=sin(
)]=sin(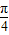 -x),故③正确;
-x),故③正确;
故答案为①②③;
点评:此题考查了命题的否定、复合命题的真假判断以及三角函数的图象,是一道基础题.
②已知p、q是简单命题,若“p∨q”为假命题,可得p与q都为假命题,然后再进行判断;
③把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移
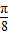 个单位,即把x变为x-
个单位,即把x变为x-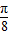 ,代入化简进行判断;
,代入化简进行判断;解答:解:①∵命题“?x∈R,使得x2+1>3x”,知“存在”的否定词为“任意”,
∴命题的否定为“?x∈R,都有x2+1≤3x”;故①正确;
②∵“p∪q”为假命题,∴p和q都为假命题,∴“¬p与¬q都为真命题,∴¬p∩¬q为真,故②正确;
③∵把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移
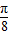 个单位,
个单位,∴y=sin[-2(x-
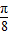 )]=sin(
)]=sin(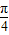 -x),故③正确;
-x),故③正确;故答案为①②③;
点评:此题考查了命题的否定、复合命题的真假判断以及三角函数的图象,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目