题目内容
已知曲线C:xy=1,过C上一点An(xn,yn)作一斜率为kn= 的直线交曲线C于另一点An+1(xn+1,yn+1),点列{An}的横坐标构成数列{xn},其中x1=
的直线交曲线C于另一点An+1(xn+1,yn+1),点列{An}的横坐标构成数列{xn},其中x1= .
.
(I)求xn与xn+1的关系式;
(II)令bn= +
+ ,求证:数列{bn}是等比数列;
,求证:数列{bn}是等比数列;
(III)若cn=3n-λbn(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有cn+1>cn成立.
(I)解:过C:xy=1上一点An(xn,yn)作斜率为kn的直线交C于另一点An+1,则kn=-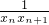
∵kn= ,∴-
,∴-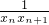 =
=
∴xnxn+1=xn+2
即: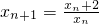
(II)证明:∵bn= +
+ ,∴bn+1=
,∴bn+1=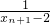 +
+ =
=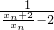 +
+ =-2(
=-2( +
+ ),
),
∵x1= ,∴b1=-2
,∴b1=-2
∴数列{bn}是等比数列.
(III)解:由(II)知, ,则cn+1>cn成立等价于cn+1-cn=2×3n+3λ×(-2)n>0恒成立
,则cn+1>cn成立等价于cn+1-cn=2×3n+3λ×(-2)n>0恒成立
即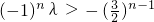 恒成立
恒成立
①n为奇数时,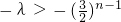 ,∴
,∴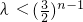 ,∴λ<1;
,∴λ<1;
②n为偶数时,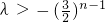 ,∴
,∴
∴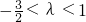
∵λ为非零整数
∴λ=-1.
∴λ=-1,对任意n∈N*,都有cn+1>cn成立.
分析:(I)由题意可得kn=-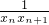 ,利用kn=
,利用kn= ,即可得到xn与xn+1的关系式;
,即可得到xn与xn+1的关系式;
(II)由bn= +
+ ,可得bn+1=-2(
,可得bn+1=-2( +
+ ),从而可得数列{bn}是等比数列.
),从而可得数列{bn}是等比数列.
(III)cn+1>cn成立等价于cn+1-cn=2×3n+3λ×(-2)n>0恒成立,即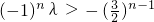 恒成立,对n讨论,即可得到结论.
恒成立,对n讨论,即可得到结论.
点评:本题考查数列递推式,考查等比数列的证明,考查恒成立问题,正确求通项是关键.
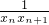
∵kn=
 ,∴-
,∴-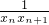 =
=
∴xnxn+1=xn+2
即:
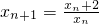
(II)证明:∵bn=
 +
+ ,∴bn+1=
,∴bn+1=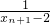 +
+ =
=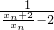 +
+ =-2(
=-2( +
+ ),
),∵x1=
 ,∴b1=-2
,∴b1=-2∴数列{bn}是等比数列.
(III)解:由(II)知,
 ,则cn+1>cn成立等价于cn+1-cn=2×3n+3λ×(-2)n>0恒成立
,则cn+1>cn成立等价于cn+1-cn=2×3n+3λ×(-2)n>0恒成立即
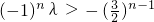 恒成立
恒成立①n为奇数时,
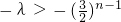 ,∴
,∴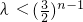 ,∴λ<1;
,∴λ<1;②n为偶数时,
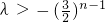 ,∴
,∴
∴
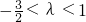
∵λ为非零整数
∴λ=-1.
∴λ=-1,对任意n∈N*,都有cn+1>cn成立.
分析:(I)由题意可得kn=-
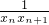 ,利用kn=
,利用kn= ,即可得到xn与xn+1的关系式;
,即可得到xn与xn+1的关系式;(II)由bn=
 +
+ ,可得bn+1=-2(
,可得bn+1=-2( +
+ ),从而可得数列{bn}是等比数列.
),从而可得数列{bn}是等比数列.(III)cn+1>cn成立等价于cn+1-cn=2×3n+3λ×(-2)n>0恒成立,即
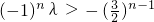 恒成立,对n讨论,即可得到结论.
恒成立,对n讨论,即可得到结论.点评:本题考查数列递推式,考查等比数列的证明,考查恒成立问题,正确求通项是关键.

练习册系列答案
相关题目