题目内容
如图,已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的两条渐近线为
的两条渐近线为 、
、 .过椭圆
.过椭圆 的右焦点
的右焦点 作直线
作直线 ,使
,使 ,又
,又 与
与 交于点
交于点 ,设
,设 与椭圆
与椭圆 的两个交点由上至下依次为
的两个交点由上至下依次为 、
、 .
.

(1)若 与
与 的夹角为
的夹角为 ,且双曲线的焦距为
,且双曲线的焦距为 ,求椭圆
,求椭圆 的方程;
的方程;
(2)求 的最大值.
的最大值.
【答案】
(1)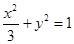 ;(2)
;(2) .
.
【解析】
试题分析:(1)先确定双曲线的渐近线方程,根据条件两条渐近线的夹角为 ,确定
,确定 与
与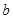 的等量关系,再结合
的等量关系,再结合 的值,确定
的值,确定 与
与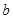 的值,最终确定椭圆
的值,最终确定椭圆 的方程;(2)设点
的方程;(2)设点 的坐标为
的坐标为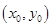 ,并设
,并设 得到
得到 ,利用向量的坐标运算得到
,利用向量的坐标运算得到 ,
, ,再由点
,再由点 在椭圆
在椭圆 上这一条件将点
上这一条件将点 的坐标代入椭圆方程,通过化简得到
的坐标代入椭圆方程,通过化简得到 与离心率
与离心率 之间的关系式
之间的关系式 ,结合基本不等式得到
,结合基本不等式得到 的最大值.
的最大值.
试题解析:(1)因为双曲线方程为 ,
,
所以双曲线的渐近线方程为 .
.
因为两渐近线的夹角为 且
且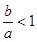 ,所以
,所以 .
.
所以
 ,所以
,所以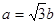 .
.

因为 ,所以
,所以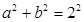 ,
,
所以 ,
, .
.
所以椭圆 的方程为
的方程为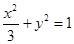 ;
;
(2)因为 ,所以直线
,所以直线 与的方程为
与的方程为 ,其中
,其中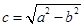 .
.
因为直线 的方程为
的方程为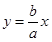 ,
,
联立直线 与
与 的方程解得点
的方程解得点 .
.
设 ,则
,则 .
.
因为点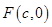 ,设点
,设点 ,则有
,则有 .
.
解得 ,
, .
.
因为点 在椭圆
在椭圆 上,
上,
所以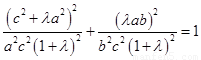 .
.
即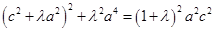 .
.
等式两边同除以 得
得 ,
, ,
,
所以 ,
,
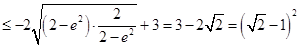
所以当 ,即
,即 时,
时, 取得最大值
取得最大值 .
.
故 的最大值为
的最大值为 .
.
考点:1.双曲线的渐近线方程;2.椭圆的方程;3.三点共线的转化

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
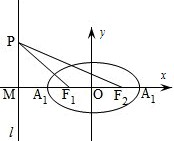 如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.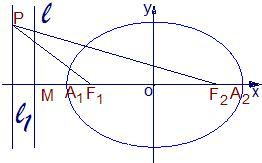 如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.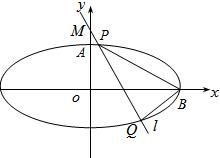 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,