题目内容
设an＝1＋q＋q2＋…＋qn－1，An＝Ca1＋Ca2＋…＋Can.
(1)用q和n表示An；
(2)又设b1＋b2＋…＋bn＝.求证：数列是等比数列．
(1)用q和n表示An；
(2)又设b1＋b2＋…＋bn＝.求证：数列是等比数列．
(1)∵q≠1，∴an＝.
∴An＝C＋C＋…＋C
＝[(C＋C＋…＋C)－(Cq＋Cq2＋…＋Cqn)]
＝[2n－(1＋q)n]．
(2)证明：∵b1＋b2＋…＋bn
＝＝，
∴b1＋b2＋…＋bn－1＝
两式相减得：bn＝n－1
∴＝≠0，
∴是等比数列．
∴An＝C＋C＋…＋C
＝[(C＋C＋…＋C)－(Cq＋Cq2＋…＋Cqn)]
＝[2n－(1＋q)n]．
(2)证明：∵b1＋b2＋…＋bn
＝＝，
∴b1＋b2＋…＋bn－1＝
两式相减得：bn＝n－1
∴＝≠0，
∴是等比数列．
略
练习册系列答案
相关题目
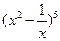的展开式中，含
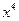的项的系数是( ) 
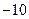
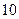
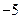
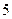
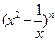展开式中, 二项式系数最大的项只有第6项, 则
=" " ( )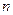