题目内容
函数 )的单调减区间为 .
)的单调减区间为 .
【答案】分析:由于f(x)=cos( -2x)=sin2x,x∈[0,π],由正弦函数的单调性即可得答案.
-2x)=sin2x,x∈[0,π],由正弦函数的单调性即可得答案.
解答:解:∵f(x)=cos(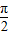 -2x)=sin2x,
-2x)=sin2x,
又x∈[0,π],
∴2x∈[0,2π];
又y=sinx在[0,2π]上的单调递减区间为:[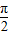 ,
,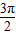 ]
]
∴由 ≤2x≤
≤2x≤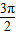 得,
得, ≤x≤
≤x≤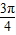 ;
;
∴f(x)=sin2x,x∈[0,π]的单调减区间为[ ,
, ].
].
故答案为:[ ,
,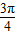 ].
].
点评:本题考查诱导公式及正弦函数的单调性,利用诱导公式将f(x)=cos(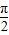 -2x)化为f(x)=sin2x,x∈[0,π]是关键,属于中档题.
-2x)化为f(x)=sin2x,x∈[0,π]是关键,属于中档题.
 -2x)=sin2x,x∈[0,π],由正弦函数的单调性即可得答案.
-2x)=sin2x,x∈[0,π],由正弦函数的单调性即可得答案.解答:解:∵f(x)=cos(
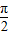 -2x)=sin2x,
-2x)=sin2x,又x∈[0,π],
∴2x∈[0,2π];
又y=sinx在[0,2π]上的单调递减区间为:[
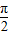 ,
,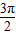 ]
]∴由
 ≤2x≤
≤2x≤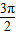 得,
得, ≤x≤
≤x≤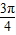 ;
;∴f(x)=sin2x,x∈[0,π]的单调减区间为[
 ,
, ].
].故答案为:[
 ,
,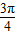 ].
].点评:本题考查诱导公式及正弦函数的单调性,利用诱导公式将f(x)=cos(
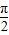 -2x)化为f(x)=sin2x,x∈[0,π]是关键,属于中档题.
-2x)化为f(x)=sin2x,x∈[0,π]是关键,属于中档题. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 则
则 的单调减区间为( )
的单调减区间为( ) B.
B.
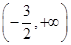 D.
D.
 ,
, 的单调减区间为( )
的单调减区间为( ) A、
A、 B、
B、 C、
C、 D、
D、
 )的单调减区间为 .
)的单调减区间为 .