题目内容
 在两道题中选择其中一道题作答,若两道都选,按前一道作答结果计分.
在两道题中选择其中一道题作答,若两道都选,按前一道作答结果计分.
(1)(几何证明选讲题)如右图所示AC和AB分别是圆O的切线,且OC=3,AB=4,延长AO到D点,则△ABD的面积是________
(2)(坐标系与参数方程题)已知圆的极坐标方程为ρ=2COSθ,则该圆的圆心到直线ρsinθ+2ρcosθ=1的距离是________.
解:(1)由题意得 AO=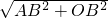 =
= =5,AD=5+3=8,设D到AB的距离等于h,
=5,AD=5+3=8,设D到AB的距离等于h,
由直角三角形相似得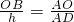 =
= ,h=
,h= .
.
故△ABD的面积等于 AB•h=
AB•h= ,
,
故答案为: .
.
(2):由ρ=2cosθ,化为直角坐标方程为x2+y2-2x=0,其圆心是A(1,0),
由ρsinθ+2ρcosθ=1得:
化为直角坐标方程为2x+y-1=0,
由点到直线的距离公式,得d=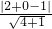 =
= .
.
故答案为 .
.
分析:(1)利用勾股定理求出AO,可得AD的值,由直角三角形相似得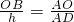 ,求出h 值,代入△ABD的面积公式进行运算.
,求出h 值,代入△ABD的面积公式进行运算.
(2)先利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,将极坐标方程为ρ=2cosθ和ρsinθ+2ρcosθ=1化成直角坐标方程,最后利用直角坐标方程的形式,结合点到直线的距离公式求解即得.
点评:(1)本题考查直线和圆相切的性质,相似三角形的性质,求出D到AB的距离等于h是解题的关键.
(2)本小题主要考查圆和直线的极坐标方程与直角坐标方程的互化,以及利用圆的几何性质计算圆心到直线的距等基本方法,属于基础题.
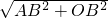 =
= =5,AD=5+3=8,设D到AB的距离等于h,
=5,AD=5+3=8,设D到AB的距离等于h,由直角三角形相似得
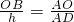 =
= ,h=
,h= .
.故△ABD的面积等于
 AB•h=
AB•h= ,
,故答案为:
 .
.(2):由ρ=2cosθ,化为直角坐标方程为x2+y2-2x=0,其圆心是A(1,0),
由ρsinθ+2ρcosθ=1得:
化为直角坐标方程为2x+y-1=0,
由点到直线的距离公式,得d=
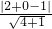 =
= .
.故答案为
 .
.分析:(1)利用勾股定理求出AO,可得AD的值,由直角三角形相似得
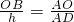 ,求出h 值,代入△ABD的面积公式进行运算.
,求出h 值,代入△ABD的面积公式进行运算.(2)先利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,将极坐标方程为ρ=2cosθ和ρsinθ+2ρcosθ=1化成直角坐标方程,最后利用直角坐标方程的形式,结合点到直线的距离公式求解即得.
点评:(1)本题考查直线和圆相切的性质,相似三角形的性质,求出D到AB的距离等于h是解题的关键.
(2)本小题主要考查圆和直线的极坐标方程与直角坐标方程的互化,以及利用圆的几何性质计算圆心到直线的距等基本方法,属于基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目