题目内容
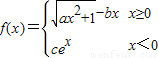 其中a>0
其中a>0(1)若f(x)在R上连续,求c
(2)若要使
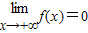 ,则a与b应满足哪些条件?
,则a与b应满足哪些条件?(3)若对于任意的a∈[2,3],f(x)是[0,+∞)的单调减函数,求b的范围.
【答案】分析:(1):由f(x)在R上连续,可得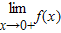 =
=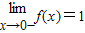 ,从而可求c
,从而可求c
(2)b<0,显然不成立,则b>0,对所求的式子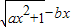 进行分子有理化,进而可求得极限为0时a,b的关系
进行分子有理化,进而可求得极限为0时a,b的关系
(3)由对于任意的a∈[2,3],f(x)是[0,+∞)的单调减函数可得f′(x)≤0在x∈[0,+∞),a∈[2,3]时恒成立,分离可得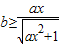 在x∈[0,+∞),a∈[2,3]时恒成立,通过求解
在x∈[0,+∞),a∈[2,3]时恒成立,通过求解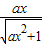 的最大值可求b的范围
的最大值可求b的范围
解答:解:(1):因为f(x)在R上连续,所以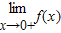 =
=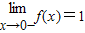
∴c=1
(2)若b<0,则显然不成立
∵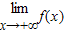 =
=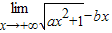 =
=
=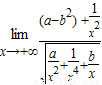
故当且仅当b>0,且a=b2时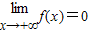
(3)∵对于任意的a∈[2,3],f(x)是[0,+∞)的单调减函数
即f′(x)≤0在x∈[0,+∞),a∈[2,3]时恒成立
∴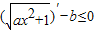
∴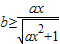 在x∈[0,+∞),a∈[2,3]时恒成立
在x∈[0,+∞),a∈[2,3]时恒成立
因为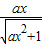 =
=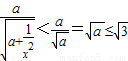
∴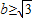
点评:本题主要考查了函数的连续的定义的应用,∞-∞型的极限的求解,一般的 处理方法是进行分子有理化,及函数的导数与函数的单调性的关系,属于函数知识的综合应用
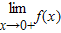 =
=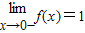 ,从而可求c
,从而可求c(2)b<0,显然不成立,则b>0,对所求的式子
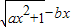 进行分子有理化,进而可求得极限为0时a,b的关系
进行分子有理化,进而可求得极限为0时a,b的关系(3)由对于任意的a∈[2,3],f(x)是[0,+∞)的单调减函数可得f′(x)≤0在x∈[0,+∞),a∈[2,3]时恒成立,分离可得
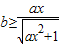 在x∈[0,+∞),a∈[2,3]时恒成立,通过求解
在x∈[0,+∞),a∈[2,3]时恒成立,通过求解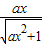 的最大值可求b的范围
的最大值可求b的范围解答:解:(1):因为f(x)在R上连续,所以
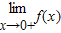 =
=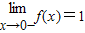
∴c=1
(2)若b<0,则显然不成立
∵
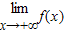 =
=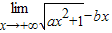 =
=
=
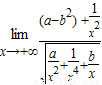
故当且仅当b>0,且a=b2时
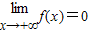
(3)∵对于任意的a∈[2,3],f(x)是[0,+∞)的单调减函数
即f′(x)≤0在x∈[0,+∞),a∈[2,3]时恒成立
∴
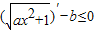
∴
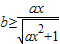 在x∈[0,+∞),a∈[2,3]时恒成立
在x∈[0,+∞),a∈[2,3]时恒成立因为
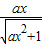 =
=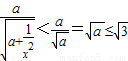
∴
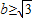
点评:本题主要考查了函数的连续的定义的应用,∞-∞型的极限的求解,一般的 处理方法是进行分子有理化,及函数的导数与函数的单调性的关系,属于函数知识的综合应用

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
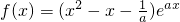 ,其中a>0
,其中a>0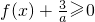 对任意x∈[0,+∞)恒成立,求a的取值范围.
对任意x∈[0,+∞)恒成立,求a的取值范围.