题目内容
设函数f(x)=x+ 的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
(1)求g(x)的解析式;
(2)若直线y=m与C2只有一个交点,求m的值和交点坐标.
 的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).(1)求g(x)的解析式;
(2)若直线y=m与C2只有一个交点,求m的值和交点坐标.
(1)g(x)=x-2+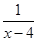 .
.
(2)当m=0时,经检验合理,交点为(3,0);
当m=4时,经检验合理,交点为(5,4).
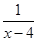 .
.(2)当m=0时,经检验合理,交点为(3,0);
当m=4时,经检验合理,交点为(5,4).
解:(1)设点P(x,y)是C2上的任意一点,则P(x,y)关于点A(2,1)对称的点为P′(4-x,2-y),代入f(x)=x+ ,
,
可得2-y=4-x+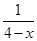 ,即y=x-2+
,即y=x-2+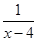 ,
,
∴g(x)=x-2+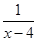 .
.
(2)由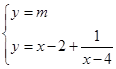
消去y得x2-(m+6)x+4m+9=0,
Δ=[-(m+6)]2-4(4m+9),
∵直线y=m与C2只有一个交点,
∴Δ=0,解得m=0或m=4.
当m=0时,经检验合理,交点为(3,0);
当m=4时,经检验合理,交点为(5,4).
 ,
,可得2-y=4-x+
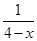 ,即y=x-2+
,即y=x-2+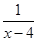 ,
,∴g(x)=x-2+
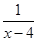 .
.(2)由
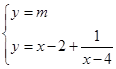
消去y得x2-(m+6)x+4m+9=0,
Δ=[-(m+6)]2-4(4m+9),
∵直线y=m与C2只有一个交点,
∴Δ=0,解得m=0或m=4.
当m=0时,经检验合理,交点为(3,0);
当m=4时,经检验合理,交点为(5,4).

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目




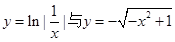 在同一平面直角坐标系内的大致图象为( )
在同一平面直角坐标系内的大致图象为( )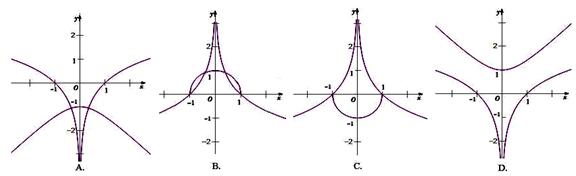
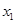 满足
满足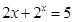 ,
,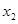 满足
满足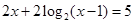 ,则
,则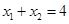 ;
;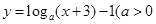 且
且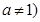 的图象恒过定点A,若A在
的图象恒过定点A,若A在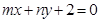 上,其中
上,其中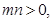 则
则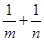 的最小值是
的最小值是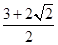 ; (3)设
; (3)设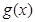 是定义在R上,以1为周期的函数,若
是定义在R上,以1为周期的函数,若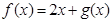 在
在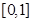 上的值域为
上的值域为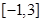 ,则
,则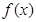 在区间
在区间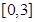 上的值域为
上的值域为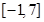 ; (4)已知曲线
; (4)已知曲线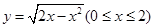 与直线
与直线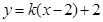 仅有2个交点,则
仅有2个交点,则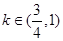 ; (5)函数
; (5)函数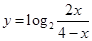 图象的对称中心为(2,1)。
图象的对称中心为(2,1)。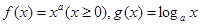 的图像可能是( )
的图像可能是( )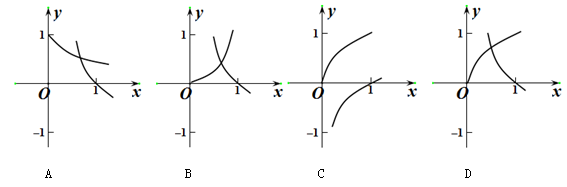
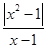 的图像与函数y=kx-2的图像恰有两个交点,则实数k的取值范围是________.
的图像与函数y=kx-2的图像恰有两个交点,则实数k的取值范围是________.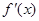 是函数
是函数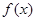 的导函数,将
的导函数,将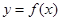 和
和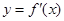 的图象画在同一个直角坐标系中,不可能正确的是()
的图象画在同一个直角坐标系中,不可能正确的是()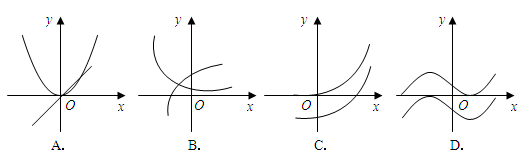
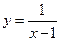 的图像与函数
的图像与函数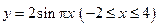 的图像所有交点的横坐标之和等于( )
的图像所有交点的横坐标之和等于( )